 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Образец решения контрольной работы № 3
|
|
Задание 1. Найти неопределенные интегралы. Результаты проверить дифференцированием.
1) 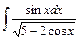 ; 2)
; 2) 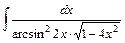 ;
;
3) 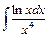 ; 4)
; 4) 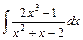 .
.
Решение. 1) Интеграл преобразуем к табличному методом замены переменной. Так как 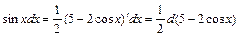 , то, вводя новую переменную
, то, вводя новую переменную 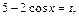 находим интеграл:
находим интеграл:
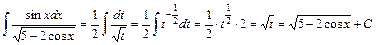 .
.
Проверка. Покажем, что производная от найденного неопределённого интеграла равна подынтегральной функции. По свойству неопределённого интеграла это означает, что интеграл найден верно.
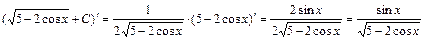 . Интеграл найден верно.
. Интеграл найден верно.
2) Преобразуем интеграл к виду 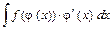 :
:
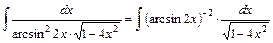 . Учитывая, что
. Учитывая, что
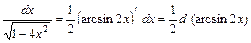 , то после введения новой переменной
, то после введения новой переменной 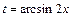 получаем табличный интеграл:
получаем табличный интеграл:
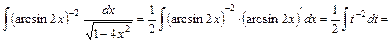
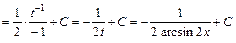 .
.
Проверка.
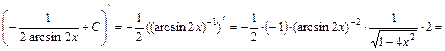
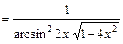 . Интеграл найден верно.
. Интеграл найден верно.
3) Для интегрирования произведения степенной функции на трансцендентную функцию (тригонометрическую, обратно тригонометрическую, показательную или логарифмическую) применяется метод интегрирования по частям, опирающийся на использование формулу интегрирования по частям 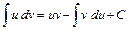 . (*)
. (*)
Пусть 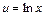 и
и 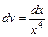 , тогда
, тогда 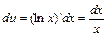 и
и 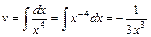 .
.
Применяя формулу (*), находим:

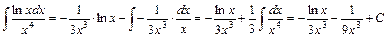 .
.
Проверка.
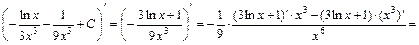
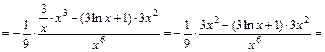
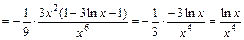 . Интеграл найден верно.
. Интеграл найден верно.
4) Для нахождения неопределённого интеграла от неправильной рациональной дроби, степень числителя которой больше или равна степени знаменателя, выделим из дроби целый многочлен и правильную дробь, используя деление многочленов «уголком»:

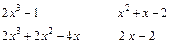
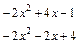

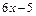
Таким образом, имеем: 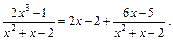
Следовательно, по свойству неопределённого интеграла
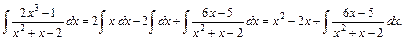 (*)
(*)
В последнем интеграле квадратный трёхчлен 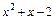 имеет два действительных корня, которые находим из квадратного уравнения
имеет два действительных корня, которые находим из квадратного уравнения 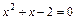 :
:
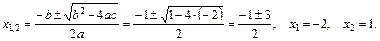
После этого правильная рациональная дробь  может быть разложена на сумму двух простейших элементарных дробей методом неопределённых (буквенных) коэффициентов следующим образом:
может быть разложена на сумму двух простейших элементарных дробей методом неопределённых (буквенных) коэффициентов следующим образом:
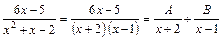 (**), где А и В – неопределённые коэффициенты.
(**), где А и В – неопределённые коэффициенты.
Приводя к общему знаменателю сумму 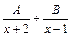 и группируя по степеням переменной х, получаем:
и группируя по степеням переменной х, получаем:
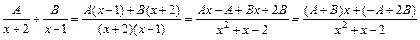 .
.
Из равенства (**) следует, что 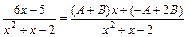 , а это возможно тогда и только тогда, когда
, а это возможно тогда и только тогда, когда 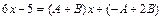 или
или 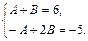 Решая систему двух линейных уравнений с двумя неизвестными, находим неопределенные коэффициенты:
Решая систему двух линейных уравнений с двумя неизвестными, находим неопределенные коэффициенты: 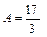 ,
, 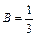 .
.
Подставим найденные значения А и В в равенство (**), получим: 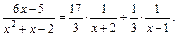
Следовательно,
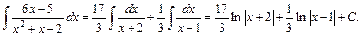
Исходный интеграл в формуле (*) примет вид:
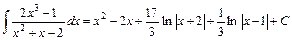 .
.
Проверка.
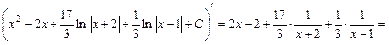
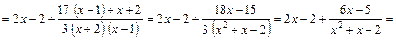
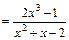 . Интеграл найден верно.
. Интеграл найден верно.
Ответ: 1) 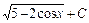 ; 2)
; 2) 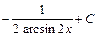 ; 3)
; 3) 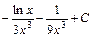 ; 4)
; 4)  .
.
Задание 2. Вычислить по формуле Ньютона-Лейбница определенный интеграл 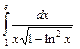 .
.
Решение. Формула Ньютона – Лейбница имеет вид:

Для вычисления заданного интеграла используем метод замены переменной в определённом интеграле: 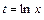 ,
, 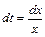 ,
, 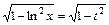 .
.
Найдём пределы интегрирования для новой переменной t. Если 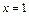 , то
, то 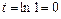 . Если
. Если 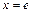 , то
, то 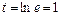 . Итак,
. Итак, 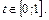 Вычисляем интеграл, переходя к новой переменной с новыми пределами интегрирования:
Вычисляем интеграл, переходя к новой переменной с новыми пределами интегрирования:
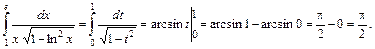
Ответ: 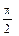 .
.
Задание 3. Вычислить площадь фигуры, ограниченной графиками функций 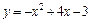 и
и 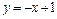 . Сделать чертеж.
. Сделать чертеж.
Решение. Для выполнения чертежа (рисунка фигуры) найдём координаты вершины параболы и точек пересечения параболы с прямой. Вершина параболы находится в точке 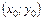 экстремума функции
экстремума функции 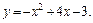 Поэтому найдём производную и приравняем её нулю.
Поэтому найдём производную и приравняем её нулю.
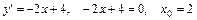
По уравнению параболы находим 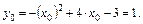 Вершина параболы находится в точке
Вершина параболы находится в точке 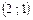 , ветви параболы направлены вниз.
, ветви параболы направлены вниз.
Для нахождения точек пересечения параболы и прямой необходимо решить систему двух уравнений:
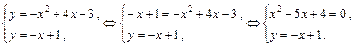

Точками пересечения являются 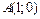 и
и 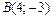 Делаем чертёж фигуры.
Делаем чертёж фигуры.
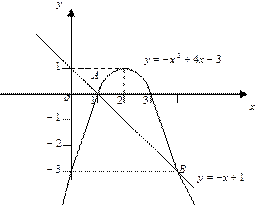 |
Для вычисления площади S полученной фигуры будем использовать формулу: 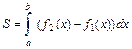 , где
, где 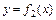 – уравнение кривой, которая ограничивает фигуру сверху, а
– уравнение кривой, которая ограничивает фигуру сверху, а 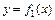 – уравнение кривой, ограничивающей фигуру снизу,
– уравнение кривой, ограничивающей фигуру снизу, 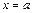 и
и 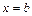 – абсциссы соответственно левой и правой точек пересечения кривых. В нашем случае:
– абсциссы соответственно левой и правой точек пересечения кривых. В нашем случае: 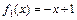 ,
, 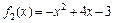 ,
, 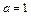 и
и  .
.
Вычисляем площадь фигуры:
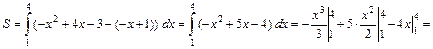
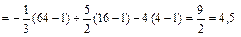 (кв. ед.).
(кв. ед.). 
Ответ: 4,5 (кв. ед.).
Задание 4. Вычислить объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной графиками функций 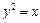 и
и 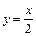 .
.
Решение. Для выполнения чертежа фигуры найдём координаты точек пересечения параболы с прямой, решив систему двух уравнений:
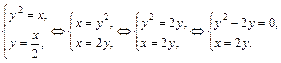
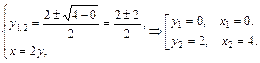
Точками пересечения являются 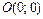 и
и 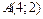 . Делаем чертёж фигуры.
. Делаем чертёж фигуры.
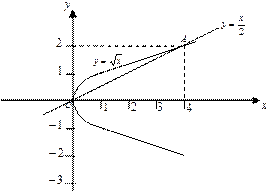 |
Для вычисления объема V, получаемого при вращении данной фигуры вокруг оси Ох, будем использовать формулу: 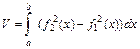 , где
, где 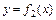 – уравнение кривой, которая ограничивает фигуру сверху, а
– уравнение кривой, которая ограничивает фигуру сверху, а 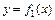 – уравнение кривой, ограничивающей фигуру снизу,
– уравнение кривой, ограничивающей фигуру снизу, 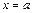 и
и 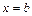 – абсциссы соответственно левой и правой точек пересечения кривых. В нашем случае:
– абсциссы соответственно левой и правой точек пересечения кривых. В нашем случае: 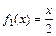 ,
, 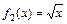 ,
, 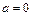 и
и  .
.
Вычисляем объем:
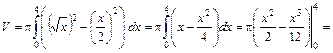
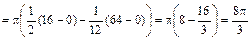 (куб. ед.).
(куб. ед.). 
Ответ:  (куб. ед.).
(куб. ед.).
4.1. Контрольная работа № 4. «Дифференциальные уравнения. Ряды».
1. Найти общее решение линейного дифференциального уравнения и частное решение, удовлетворяющее начальному условию y (x 0) = y 0.
1. 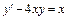 ,
, 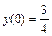 . 2.
. 2. 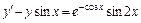 ,
, 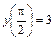 .
.
3.  , y (0) = 5. 4.
, y (0) = 5. 4. 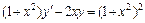 , y (–2) = 5.
, y (–2) = 5.
5. 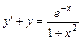 , y (0) = 2. 6.
, y (0) = 2. 6. 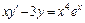 , y (1) = e.
, y (1) = e.
7. 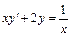 , y (3) = 1. 8.
, y (3) = 1. 8. 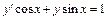 , y (0) = 2.
, y (0) = 2.
9.  , y (1) = 0. 10.
, y (1) = 0. 10. 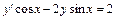 , y (0) = 3.
, y (0) = 3.
2. Найти общее решение линейного неоднородного дифференциального уравнения 2-го порядка с постоянными коэффициентами с правой частью специального вида и частное решение, удовлетворяющее начальным условиям y (x 0) = y 0 и 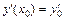
1. 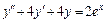 , y (0) = –2,
, y (0) = –2, 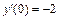 .
.
2. 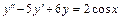 , y (0) = 3,
, y (0) = 3, 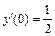 .
.
3. 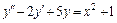 , y (0) = –3,
, y (0) = –3, 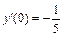 .
.
4. 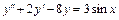 , y (0) = –1,
, y (0) = –1, 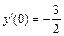 .
.
5. 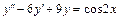 , y (0) = 1,
, y (0) = 1, 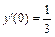 .
.
6. 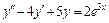 , y (0) = 2,
, y (0) = 2, 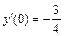 .
.
7. 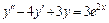 , y (0) = 2,
, y (0) = 2, 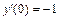 .
.
8. 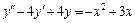 , y (0) = 3,
, y (0) = 3, 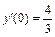 .
.
9. 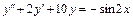 , y (0) = 0,
, y (0) = 0, 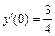 .
.
10. 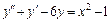 , y (0) = 0,
, y (0) = 0, 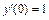 .
.
3. Написать три первых члена степенного ряда, найти его область абсолютной сходимости.
1. 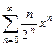 . 2.
. 2. 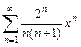 . 3.
. 3. 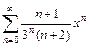 .
.
4.  . 5.
. 5. 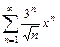 . 6.
. 6. 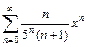 .
.
7. 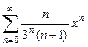 . 8.
. 8. 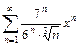 . 9.
. 9. 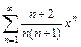 .
.
10. 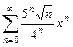 .
.
4. Вычислить определенный интеграл с точностью до 0,001, разложив подынтегральную функцию в степенной ряд.
1. 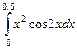 . 2.
. 2. 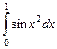 . 3.
. 3. 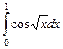 .
.
4. 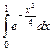 . 5.
. 5. 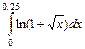 . 6.
. 6. 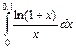 .
.
7. 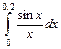 . 8.
. 8. 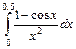 . 9.
. 9. 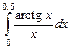 .
.
10. 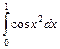 .
.
Дата публикования: 2014-11-04; Прочитано: 328 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
