Положительные числовые ряды

4. Первый признак сравнения рядов. Пусть даны два положительных ряда и . Если, начиная с некоторого номера n, выполняется условие , то:

1) из сходимости ряда следует сходимость ряда ;

2) из расходимости ряда следует расходимость ряда .

5. Второй признак сравнения рядов. Пусть даны два положительных ряда и . Если существует , то оба ряда ведут себя одинаково.

6. При использовании признаков сравнения чаще всего используют эталонные ряды:

1) Геометрический ряд a + aq + aq ² + … + aq^{n – 1} + … = сходится при и расходится при .

2) Ряд Дирихле сходится при и расходится при .

3) Частный случай ряда Дирихле при p = 1 – гармонический ряд расходится.

7. Признак Даламбера. Пусть дан положительный ряд и существует предел . Тогда:

1) если , то ряд сходится;

2) если , то ряд расходится;

3) если , то вопрос о сходимости ряда остается открытым.

8. Радикальный признак Коши. Пусть дан положительный ряд и существует предел . Тогда:

1) если , то ряд сходится;

2) если , то ряд расходится;

3) если , то вопрос о сходимости ряда остается открытым.

9. Интегральный признак Коши. Пусть дан положительный ряд . Если существует непрерывная, невозрастающая и неотрицательная функция на такая, что 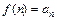, то ряд и несобственный интеграл ведут себя одинаково.