 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Основные теоретические сведения. Неопределенный интеграл
|
|
Неопределенный интеграл
1. Неопределенным интегралом функции f (x) называется множество всех ее первообразных F (x) + C и обозначается символом  , где функция F (x) называется первообразной функции f (x):
, где функция F (x) называется первообразной функции f (x):  .
.
Основные свойства неопределенного интеграла
2.  . 3.
. 3. 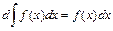 .
.
4.  . 5.
. 5.  .
.
6. Если  , то
, то  .
.
Таблица интегралов
7.  . 8.
. 8.  .
.
9.  . 10.
. 10.  .
.
11.  . 12.
. 12.  .
.
13.  . 14.
. 14.  .
.
15.  . 16.
. 16.  .
.
17.  . 18.
. 18.  .
.
19. 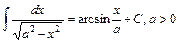 . 20.
. 20.  .
.
21. 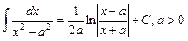 . 22.
. 22.  .
.
23. 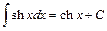 . 24.
. 24.  .
.
25. Теорема о замене переменной в неопределенном интеграле: пусть требуется найти интеграл от сложной функции вида 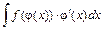 , тогда если заменой
, тогда если заменой  ,
,  интеграл сводится к табличному
интеграл сводится к табличному  , то справедлива формула
, то справедлива формула  .
.
26. Формула интегрирования по частям:  .
.
27. Некоторые интегралы, вычисляемые по частям:
| 1-я группа | 2-я группа | ||||
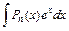
| u = Pn (x) | 
| 
| 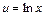
| dv = Pn (x) |

| 
| 
| 
| ||
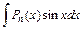
| 
| 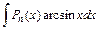
| 
| ||

| 
| 
| 
| ||

| 
| ||||
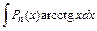
| 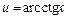
|
3-я группа:  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  и др.
и др.
Дата публикования: 2014-11-04; Прочитано: 297 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
