Приложения определенного интеграла в геометрии

5. Площадь криволинейной трапеции в декартовой прямоугольной системе координат (рис. 8) вычисляется по формуле: 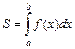. Если на (график функции лежит ниже оси 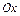), то .

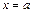6. Если криволинейная трапеция ограничена сверху кривой, заданной параметрически то площадь фигуры равна: , где и соответствуют значениям и .

7. Площадь криволинейного сектора, ограниченного кривой 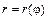и двумя лучами и 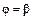в полярных координатах (рис. 9) вычисляется по формуле: .

8. Если кривая задана уравнением 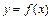в декартовой прямоугольной системе координат, то длина этой кривой от точки до точки вычисляется по формуле: . Если кривая определяется уравнением , то .

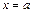9. Если кривая задана параметрически , то длина кривой вычисляется по формуле: , где и соответствуют значениям и .

10. Если кривая задана уравнением 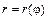в полярных координатах, то ее длина между лучами и 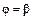равна: .

11. Объем тела, образованного вращением вокруг оси 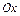криволинейной трапеции (рис. 8), вычисляется по формуле: . Если эту криволинейную трапецию вращать вокруг оси , то объем тела вращения равен , причем .

12. Если криволинейная трапеция ограничена кривой (), осью и прямыми и (рис. 10), то объем полученного тела вращения вокруг оси равен: .

Рис. 10

13. Если дуга кривой, заданная в декартовых прямоугольных координатах 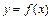, где , вращается вокруг оси 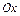, то площадь поверхности вращения вычисляется по формуле: .

14. Если дуга кривой , где вращается вокруг оси , то площадь поверхности вращения вычисляется по формуле: .

15. Если дуга кривой задана параметрически где , то площадь поверхности вращения вокруг оси 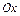равна: .

16. Если дуга задана в полярных координатах 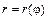, где , то .