Знакопеременные и знакочередующиеся ряды

10. Признак Лейбница. Пусть дан знакочередующийся ряд , где a_n > 0. Если 1) члены знакочередующегося ряда убывают по абсолютной величине и 2) предел его общего члена при 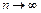равен нулю, т. е. 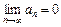, то исходный ряд сходится, а его сумма не превосходит первого члена .

11. Пусть дан знакопеременный ряд . Если соответствующий ряд сходится, то данный ряд сходится абсолютно.

12. Если знакопеременный ряд сходится по признаку Лейбница, а соответствующий ряд расходится, то данный ряд сходится условно.