Свойства операций. Проверим это свойство для матриц и

1^о .

Проверим это свойство для матриц и .

, .

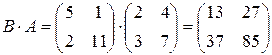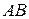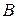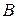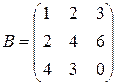На самом деле может случиться так, что произведение существует, а не существует (это связано с тем, что операция умножения матриц и определена только для того случая, когда число столбцов матрицы равно числу строк матрицы ). Например, матрицу можно умножить на , а найти произведение – невозможно. Однако, в частном случае равенство возможно, например, для матриц и . (Поверьте).

2^о .

3^о .

4^о .

5^о .

6^о .

5) Если в матрице поменять местами строки и столбцы, то новая матрица называется транспонированной по отношению к матрице :

; .

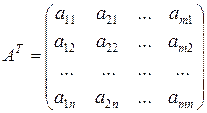Пример 2.5. Для матрицы запишите соответствующую ей транспонированную.

Решение. Поменяем местами строки и столбцы

.