 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Решение. 4) Произведением матрицы размерности на матрицу
|
|
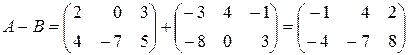 .
.
4) Произведением матрицы  размерности
размерности 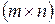 на матрицу
на матрицу 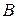 размерности
размерности 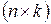 называется матрица
называется матрица 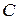 размерности
размерности 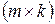 , каждый элемент которой равен сумме произведений элементов
, каждый элемент которой равен сумме произведений элементов  -той строки матрицы
-той строки матрицы  на соответствующие элементы
на соответствующие элементы 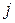 -того столбца матрицы
-того столбца матрицы 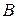 .
.
Замечание: Правило умножения матрицы  на матрицу
на матрицу 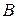 определяется только для случая, когда число столбцов матрицы
определяется только для случая, когда число столбцов матрицы  равно числу строк матрицы
равно числу строк матрицы 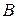 .
.
Поясним правило умножения матриц примерами. Для начала покажем умножение строки на столбец:
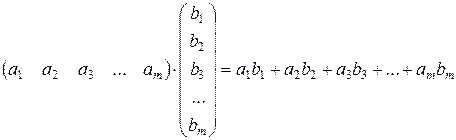 ,
,
т.е. их результат есть число. Аналогичным образом находится каждый элемент матрицы. Например, требуется перемножить матрицы
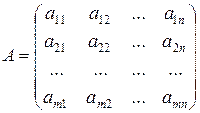 и
и 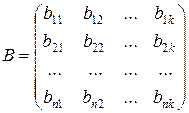 .
.
В результате получим матрицу
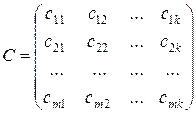 ,
,
каждый элемент которой мы находим по формуле
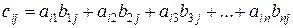 ,
,
то есть для того, чтобы найти элемент 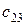 мы элементы второй строки матрицы
мы элементы второй строки матрицы  умножаем на элементы третьего столбца матрицы
умножаем на элементы третьего столбца матрицы 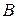 и складываем между собой.
и складываем между собой.
Примеры 2.4.:
а) 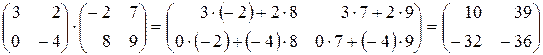 .
.
б) 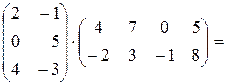
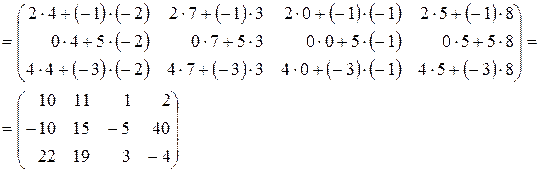
в) Даны матрицы 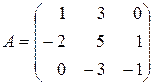 и
и 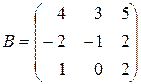 . Найти матрицу
. Найти матрицу 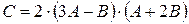 .
.
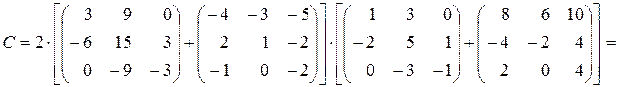
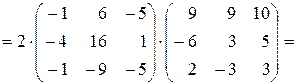
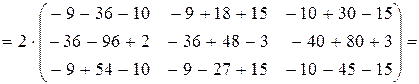
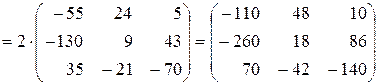 .
.
Дата публикования: 2014-11-04; Прочитано: 620 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
