 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Введение. Создание в ХVIII веке теории матриц и определителей было связано с изучением систем линейных уравнений
|
|
Создание в ХVIII веке теории матриц и определителей было связано с изучением систем линейных уравнений. Для таких систем были получены формулы, позволяющие выразить решения через коэффициенты при неизвестных и свободные члены.
В ХІХ веке У. Гамильтон, Г. Грассман и другие математики в своих работах ввели векторы, хотя до этого они встречались в трудах Архимеда, Г. Галилея и других корифеев науки, но имели на тот момент только механический смысл.
Применяемые в рамках евклидовой геометрии векторные методы значительно упрощают доказательства многих теорем и решение задач. Например, теорема косинусов, теорема о трех перпендикулярах и другие, которые изучались в школьном курсе, имели довольно громоздкие доказательства, а применение скалярного произведения векторов значительно упрощает процесс доказательства.
Но роль векторов состоит не только в упрощении трудных мест школьного курса. Гораздо важнее то, что векторные методы находят сейчас широкое применение в физике, химии, экономике, биологии, не говоря уже о многих разделах современной математики. Студентам специальности «Оборудование» интересно будет узнать, что скалярное произведение вектора силы и вектора перемещения представляет собой работу, выполненную силой по перемещению материальной точки; а векторное произведение вектора тока и вектора напряженности магнитного поля – силу воздействия этого поля на проводник и т.д.
Впоследствии при рассмотрении многомерных пространств, скалярное произведение приобрело еще большее значение и стало мощным рабочим инструментом, применяемым буквально во всех областях математики и ее приложениях.
Целью данной методической разработки является оказание помощи студентам в освоении таких тем как матрицы и векторы. Эти темы не случайно объединены: они являются одними из первых, которые изучаются на первом курсе специальностей ОБ, ТН и др., кроме того они тесно связаны между собой. Например, нахождение векторного или смешанного произведений требуют наличия определенных знаний по вычислению определителя, решение систем линейных уравнений основывается на знании способов вычисления определителей и умении производить необходимые действия над матрицами и т.д.
Самостоятельную работу в соответствии с этой методической разработкой студентам рекомендуется проводить в следующем порядке:
Ø прочитать теоретический материал и разобрать решение типовых задач (лучше, если потом эти задания будут решены самостоятельно);
Ø решить задания проверочного теста;
Ø проверить свои результаты, сравнив с ответами теста;
Ø если ответы не совпадают или решение каких-либо задач вызвало трудность, то с помощью методических указаний следует вновь обратиться к теоретическому материалу;
Ø решить контрольную работу по своему варианту, тем самым закрепив свои знания.
| I. М а т р и ц ы |
Основные понятия
Матрицей называется множество чисел, записанных в виде прямоугольной таблицы, имеющей  строк и
строк и  столбцов. Числа, составляющие матрицу, называются ее элементами.
столбцов. Числа, составляющие матрицу, называются ее элементами.
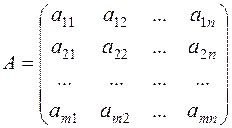 .
.
Для сокращения записи матрицу можно представить в компактном виде 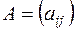 , (
, (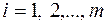 ;
;  ), где индекс
), где индекс  обозначает номер строки, индекс
обозначает номер строки, индекс 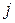 – номер столбца матрицы.
– номер столбца матрицы.
Матрица, имеющая  строк и
строк и  столбцов, называется матрицей размера
столбцов, называется матрицей размера  .
.
Если число строк матрицы равно числу столбцов 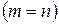 , то матрица называется квадратной порядка
, то матрица называется квадратной порядка  .
.
Среди квадратных матриц отметим диагональные матрицы, у которых все элементы с неравными индексами 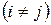 равны нулю:
равны нулю:
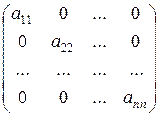 .
.
Элементы 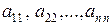 расположены на главной диагонали.
расположены на главной диагонали.
Диагональные матрицы, все отличные от нуля элементы которых равны между собой 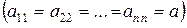 , называются скалярными матрицами. Если
, называются скалярными матрицами. Если 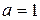 , то скалярная матрица называется единичной. Единичную матрицу принято обозначать буквой
, то скалярная матрица называется единичной. Единичную матрицу принято обозначать буквой 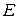 :
:
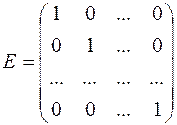 .
.
Матрица  , все элементы которой равны нулю, называется нулевой, и ее обозначают 0:
, все элементы которой равны нулю, называется нулевой, и ее обозначают 0:
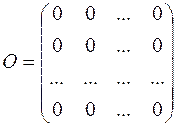 .
.
Две матрицы 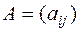 и
и 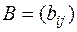 одного и того же размера называются равными, если все их соответствующие элементы равны. Т.е.
одного и того же размера называются равными, если все их соответствующие элементы равны. Т.е. 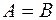 , если
, если 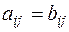 для всех
для всех  и
и 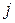 .
.
Дата публикования: 2014-11-04; Прочитано: 568 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
