Определенный интеграл с переменным верхним пределом

Пусть - непрерывная на отрезке функция, а - ее первообразная. Рассмотрим определенный интеграл

, (10.2)

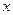где . При изменении меняется и определенный интеграл (10.2), т.е. он является функцией верхнего предела интегрирования 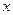, которую обозначим через :

, (10.3)

Определение. Функция называется интегралом с переменным верхним пределом (с открытым верхним пределом).

Теорема 1. Если функция непрерывна на отрезке 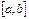то функция так же непрерывна на .

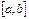Теорема 2 (о производной интеграла по верхнему пределу). Пусть функция непрерывна на отрезке 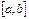. Тогда в каждой точке 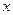отрезка 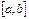производная функции по переменному верхнему пределу равна подынтегральной функции на верхнем пределе, т.е.

.