Задачи с решениями. Задача 1. Найдите производную скалярного поля в точке по направлению вектора , если

Задача 1. Найдите производную скалярного поля 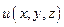в точке по направлению вектора , если

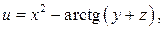
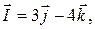
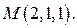
Решение. Производная скалярного поля 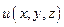в точке 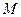по направлению вектор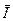а равна

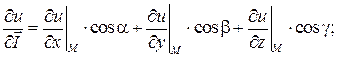
вычислим

,

,

,

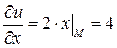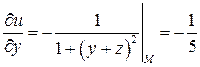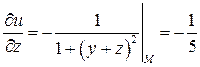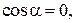
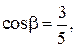
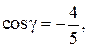
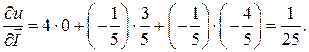
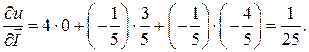
Ответ: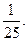

Задача 2. Найдите угол между градиентами скалярных поле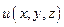й и 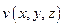в точке 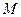, если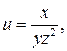

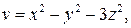
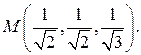
Решение. Градиент скалярного поля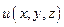

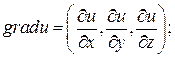
вычислим

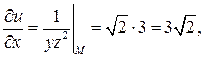
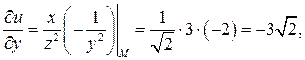
Таким образом,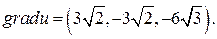

Градиент скалярного поля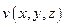

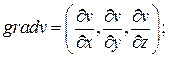
Вычислим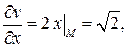

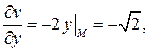
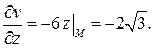
Таким образом,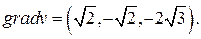

Вычислим косинус угла 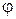между градиентами скалярных поле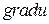й и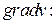

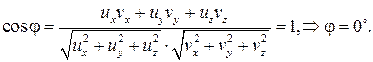
Ответ: 0.

Задача 3. Найдите векторные линии в векторном поле .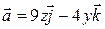

Решение. Векторные линии для векторного поля 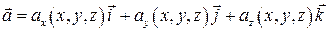описываются системой дифференциальных уравнени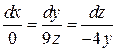й или 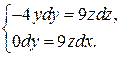Интегрируя, получаем 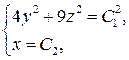то есть векторные линии этого поля представляют собой эллипсы с центрами на оси 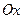, лежащие в плоскостях, перпендикулярных к этой оси.

Ответ: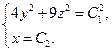

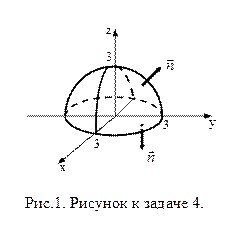
Задача 4. Найдите поток векторного поля 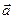через часть поверхности 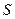, вырезаемую плоскостью 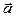(нормаль внешняя к замкнутой поверхности, образуемой данными поверхностями), если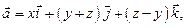

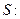
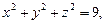
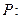
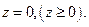
Решение

Поток 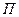векторного поля 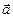через часть поверхности сферы 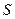радиусом 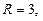с центром в начале координат, ограниченную плоскостью 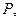вычислим как разность потока 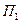через замкнутую поверхность, состоящую из полусферы и ограничивающей ее плоскости и потока 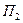через данную часть плоскости.

Для вычисления потока 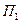воспользуемся теоремой Гаусса – Остроградского:

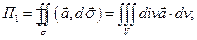здесь 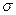- полученная полная поверхность, 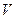- ограниченное ею тело (полушар).

Вычислим 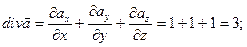откуда

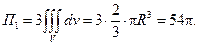
Вычислим поток 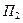через круг, лежащий в основании полушара , в направлении внешней к полушару нормали :

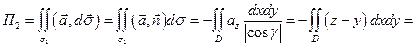
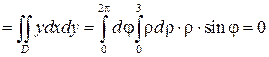
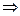
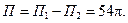
Ответ: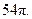

Задача 5. Найдите поток векторного поля 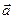через часть плоскости 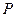, расположенной в первом октанте (нормаль образует острый угол с осью 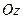), если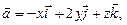

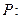
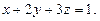
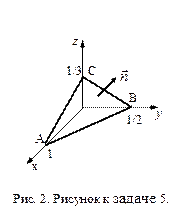Решение. Запишем уравнение плоскости 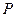"в отрезках": 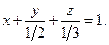Из него видно, что точки пересечения плоскости 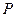с координатными осями есть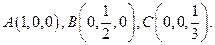

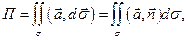
где 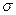- часть плоскости 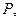расположенная в первом октанте,

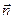- единичный вектор нормали к плоскости 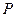. Запишем уравнение плоскости 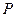в виде 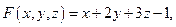тогда

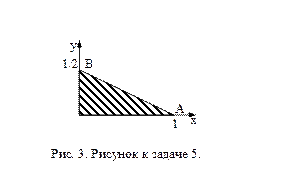
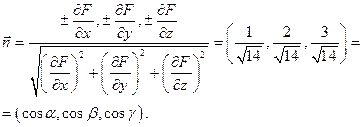
(Нормаль образует острые углы с осями координат, поэтому следует выбрать знаки "+" во всех случаях.) Отсюда

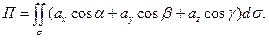
Произведем проецирование на координатную плоскость 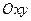, 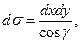поэтому

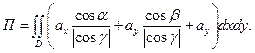
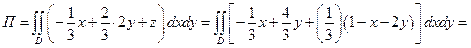
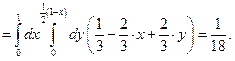
Ответ: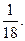

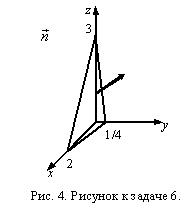Задача 6. Найдите поток векторного поля 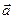через часть плоскости 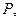расположенной в первом октанте (нормаль образует острый угол с осью Oz), если

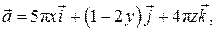
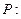
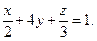
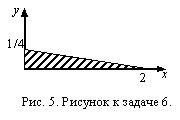
Решение

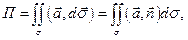перейдем к двойному интегралу по области 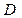в плоскости (см. задачу 5)

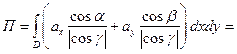
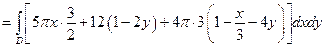, перейдем к повторному интегралу

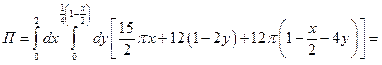
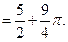
Ответ:

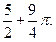
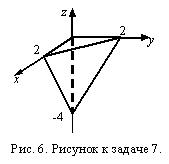
Задача 7. Найдите поток векторного поля 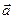через замкнутую поверхность 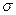(нормаль внешняя), если

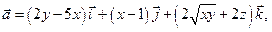
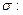
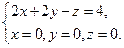
Решение Уравнение плоскости "в отрезках"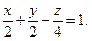

Поток 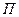векторного поля 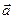через замкнутую поверхность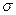

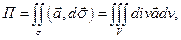
вычислим 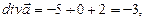поэтому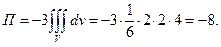

Ответ: -8.

Задача 8. Найдите поток векторного поля 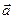через замкнутую поверхность 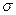в направлении внешней нормали, если

:

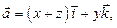
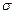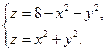
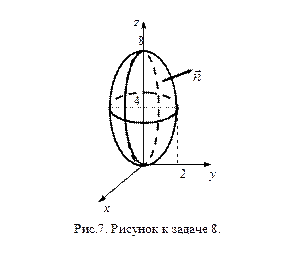Решение. Поток векторного поля 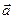через замкнутую поверхность 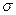в направлении внешней нормали

где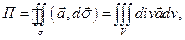

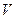- тело, ограниченное замкнутой поверхностью 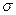(общей частью пары однополостных гиперболоидов); вычислим 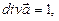поэтому

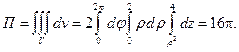
Ответ: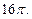

Задача 9. Найдите поток векторного поля 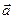через замкнутую поверхность 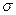в направлении внешней нормали, если

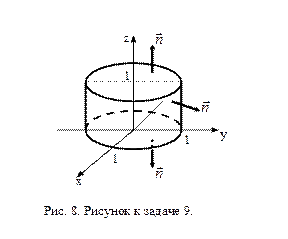
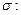
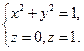
Решение. Поток векторного поля 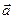через замкнутую поверхность 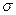в направлении внешней нормали

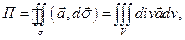
вычислим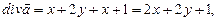

поэтому

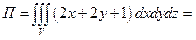
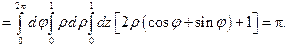
Ответ: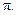

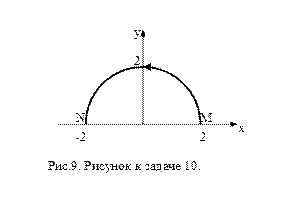
Задача 10. Найдите работу силы 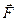при перемещении вдоль линии 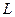от точки 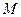к точке , если

,

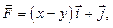
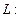
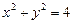
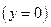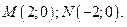
Решение.

Уравнения кривой 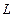в параметрическом виде 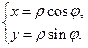Работа силы 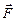при перемещении вдоль линии 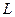от точки 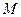к точке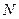

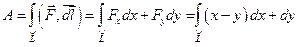. Перейдем к параметрическому заданию кривой 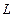: 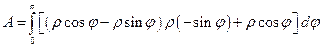. Подставим значение 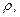равное 2. Тогда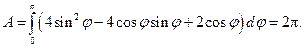

Ответ: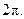

Задача 11. Найдите циркуляцию векторного поля 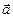вдоль контура 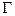(в направлении, соответствующем возрастанию параметра 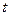), если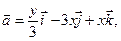

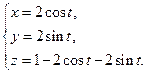
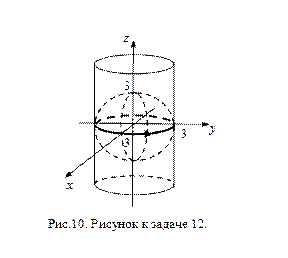Решение. Линия 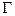- замкнутая, с периодом 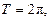проекция линии 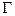на плоскость 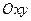представляет собой окружность радиусом 2 с центром в начале координат.
,
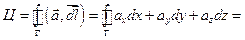
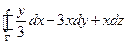перейдем к параметрическому заданию кривой :

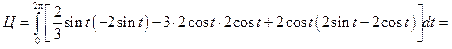
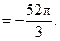
Ответ: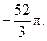

Задача 12. Найдите модуль циркуляции векторного поля 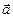вдоль контура 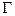, если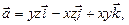

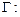
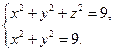
Решение.

Первый способ. Перепишем уравнение кривой 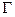в виде

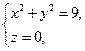или, в параметрическом виде,

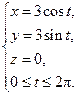
Тогда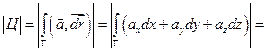

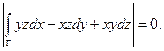
(Здесь мы учли, что z=0).

Ответ: 0.

Второй способ

Перепишем уравнения, задающие кривую 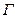в виде 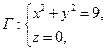воспользуемся теоремой Стокса:

Циркуляция вектора 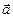по замкнутому контуру 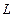равна потоку вектора 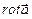через поверхность 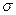, ограниченную этим контуром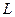

Ц= .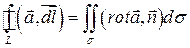

Вычислим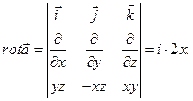

Отсюда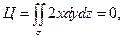

так как 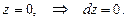Таким образом,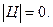

Ответ: 0.