 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Площадь поверхности
|
|
Пусть 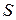 - незамкнутая гладкая поверхность. Разобьем ее на участки
- незамкнутая гладкая поверхность. Разобьем ее на участки 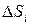 , (
, (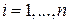 ), с помощью сети кривых. Выберем в каждом участке
), с помощью сети кривых. Выберем в каждом участке 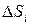 точку
точку 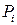 . Проведем в точке
. Проведем в точке 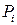 касательную плоскость к поверхности
касательную плоскость к поверхности 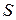 и спроектируем
и спроектируем 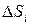 на касательную плоскость. На проекции получим плоскую фигуру с площадью
на касательную плоскость. На проекции получим плоскую фигуру с площадью 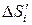 .
.
ОПРЕДЕЛЕНИЕ. Площадью поверхности 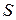 называется предел суммы площадей
называется предел суммы площадей 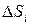 (
(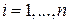 ) при условии, что диаметры всех частей разбиения
) при условии, что диаметры всех частей разбиения 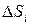 стремятся к нулю:
стремятся к нулю: 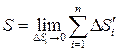 .
.
Поверхность, имеющая площадь, называется квадрируемой.
Пусть поверхность задается явным уравнением 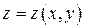 , где
, где 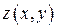 - непрерывно дифференцируемая функция, и однозначно проектируется в плоскую область
- непрерывно дифференцируемая функция, и однозначно проектируется в плоскую область 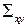 на координатной плоскости
на координатной плоскости  . Нормаль
. Нормаль 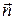 к поверхности
к поверхности 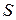 , как вектор, ортогональный к касательной плоскости, имеет компоненты:
, как вектор, ортогональный к касательной плоскости, имеет компоненты: 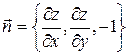 , и направляющие косинусы нормали
, и направляющие косинусы нормали 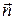 равны:
равны:
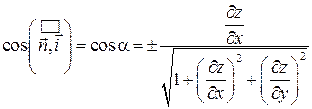 ,
,
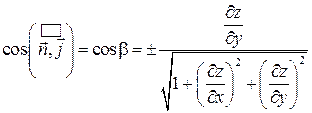 ,
,
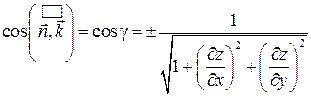 .
.
Выбор знака перед радикалом соответствует острому или тупому углу нормали 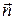 с соответствующей осью координат и определяет сторону поверхности
с соответствующей осью координат и определяет сторону поверхности 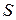 .
.
Спроектируем элементы 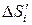 на касательной плоскости на координатную плоскость
на касательной плоскости на координатную плоскость  ; площадь проекции
; площадь проекции
 .
.
Следовательно,
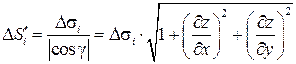 ,
,
и предел, фигурирующий в определении площади поверхности 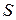 , представляет собой двойной интеграл по области
, представляет собой двойной интеграл по области 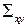
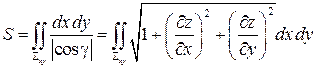 .
.
Если уравнение поверхности 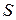 дано в виде
дано в виде 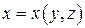 или
или 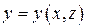 , то площадь может быть представлена как
, то площадь может быть представлена как

или
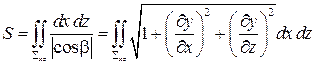 ,
,
где 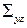 и
и  - проекции поверхности
- проекции поверхности 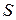 на плоскости
на плоскости 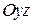 и
и 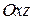 .
.
Дата публикования: 2014-11-04; Прочитано: 502 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
