 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Вычисление поверхностных интегралов 1-го рода
|
|
Вычислим  . Пусть . Пусть 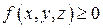 , а поверхность , а поверхность  задана уравнением задана уравнением 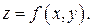 Лемма. Площадь проекции плоского участка одной плоскости
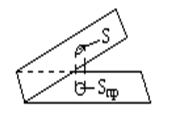
Лемма. Площадь проекции плоского участка одной плоскости  на другую на другую 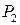 равна площади самого участка, умноженной на модуль косинуса двугранного угла между плоскостями: равна площади самого участка, умноженной на модуль косинуса двугранного угла между плоскостями:  .
Доказательство: .
Доказательство:
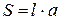  (поскольку (поскольку 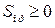 , косинус берется по модулю). , косинус берется по модулю).
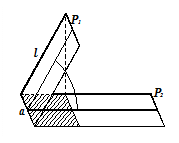
 Пусть требуется вычислить поверхностный интеграл 1-го рода по поверхности Пусть требуется вычислить поверхностный интеграл 1-го рода по поверхности 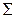 . Область . Область 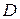 является проекцией поверхности является проекцией поверхности 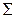 на плоскость на плоскость 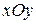 . Через точку . Через точку  проведем касательную плоскость. Ее уравнение: проведем касательную плоскость. Ее уравнение:  . Выберем часть поверхности . Выберем часть поверхности 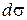 и спроектируем ее на касательную плоскость. Обозначим проекцию и спроектируем ее на касательную плоскость. Обозначим проекцию 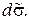 Будем считать Будем считать  . Обозначим . Обозначим 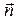 - нормаль к плоскости: - нормаль к плоскости: 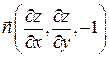 . Поскольку . Поскольку 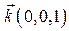 - нормаль к - нормаль к  , то угол , то угол  - угол между касательной плоскостью и плоскостью - угол между касательной плоскостью и плоскостью  , он равен углу между векторами , он равен углу между векторами 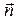 и и 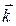 . .
| 
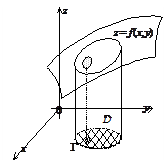
|
Найдем связь между  (проекцией
(проекцией 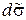 на плоскость
на плоскость 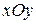 ) и
) и 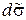
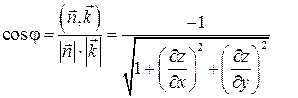 ;
; 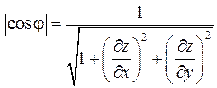
в пределе при 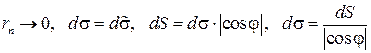 ;
;
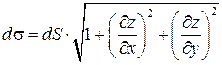 ;
;
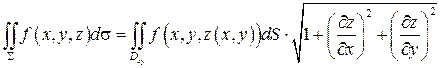 .
.
Так записывается поверхностный интеграл, если поверхность задана уравнением 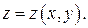
Если поверхность задана уравнением  то
то
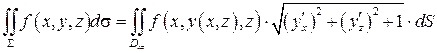 .
.
Аналогично, если 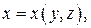 то
то
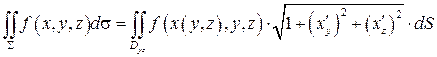 ,
,
где 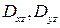 - проекции
- проекции  на плоскости
на плоскости 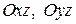 .
.
Итак, для поверхности 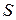 , в каждой точке которой задана функция:
, в каждой точке которой задана функция: 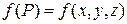 , если поверхность однозначно проектируется на плоскость
, если поверхность однозначно проектируется на плоскость  в область
в область 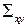 и задана уравнением
и задана уравнением 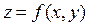 , то
, то

 .
.
Дата публикования: 2014-11-04; Прочитано: 378 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
