 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Поверхностный интеграл 2-го рода
|
|
Рассмотрим ориентированную поверхность 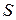 . Спроектируем элемент поверхности
. Спроектируем элемент поверхности 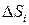 на координатную плоскость
на координатную плоскость  . Составим интегральную сумму произведений значений функции в произвольной точке
. Составим интегральную сумму произведений значений функции в произвольной точке 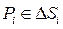 на величину площади проекции части
на величину площади проекции части 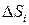 на координатную плоскость
на координатную плоскость 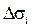 :
:
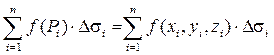 .
.
Конечный предел этой интегральной суммы при стремлении диаметра разбиения к нулю называется поверхностным интегралом 2-го рода от функции 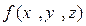 по определенной стороне поверхности и обозначается:
по определенной стороне поверхности и обозначается:
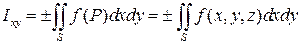 .
.
Знак (+) соответствует положительной (внешней), а (–) отрицательной (внутренней) сторонам поверхности.
Если на данной поверхности заданы другие функции 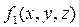 ,
, 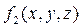 , то проектирование на другие координатные плоскости дает интегралы:
, то проектирование на другие координатные плоскости дает интегралы:
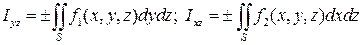 .
.
Соединение этих интегралов дает общее выражение для поверхностного интеграла 2-го рода:
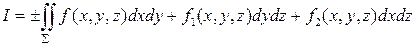 .
.
Между поверхностными интегралами 1-го и 2-го рода существует следующая связь:
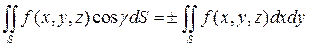 ,
,
причем при интегрировании по положительной стороне поверхности:
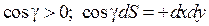 ,
,
а по отрицательной:  .
.
Поверхностные интегралы 2-го рода обладают всеми свойствами двойных интегралов.
Поверхностный интеграл 2-го рода может быть также записан в более компактном виде. Пусть 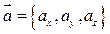 , где
, где 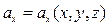 ,
, 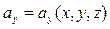 ,
,  - векторное поле. Составим для координат этого вектора поверхностный интеграл 2-го рода.
- векторное поле. Составим для координат этого вектора поверхностный интеграл 2-го рода.

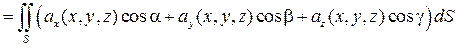 .
.
Так как 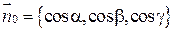 ,
, 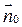 - единичный вектор нормали к выбранной стороне поверхности
- единичный вектор нормали к выбранной стороне поверхности 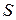 , то
, то 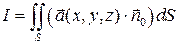 .
.
Вводя 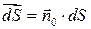 - векторный элемент площади, направленный по нормали
- векторный элемент площади, направленный по нормали 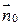 и имеющий длину
и имеющий длину 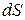 , получаем
, получаем 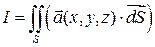 .
.
Дата публикования: 2014-11-04; Прочитано: 288 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
