Свойства градиента

Пусть задан градиент поля и производная по направлению:

, = .

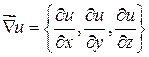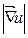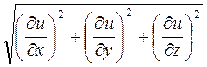1. Максимальное значение производной по направлению равно модулю градиента: ; .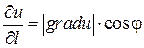

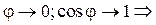
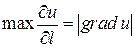2. Вектор 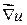направлен в сторону возрастания поля.

3. Вектор 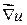всегда нормален к поверхности (линии) уровня поля (эквипотенциальной поверхности).

Доказательство:

Пусть 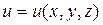скалярное поле и 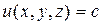- уравнение поверхности уровня. Выберем 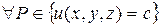, которую обозначим 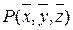, и проведём касательную плоскость к поверхности, описываемой уравнением

;

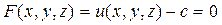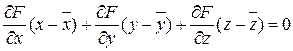- уравнение касательной плоскости;

.

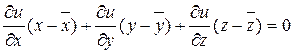Тогда вектор нормали касательной плоскости имеет вид:

, .

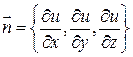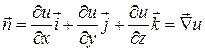Свойства 1-3 дают инвариантное (не зависящее от системы координат) определение градиента, т.е. утверждают, что независимо от системы координат 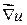указывает величину и направление наибольшего возрастания скалярного поля в точке: 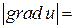max .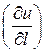

Дифференциальные свойства градиента:

· Если скалярное поле есть сумма двух полей

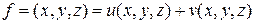, то .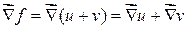

· .

· .

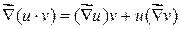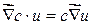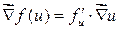· - градиент сложной функции.

· .

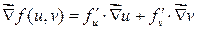ПРИМЕР. Найдите наибольшую крутизну подъёма поверхности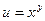

в точке Р (2,2,4).

Решение: 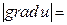max .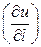

= .

.

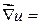
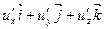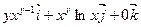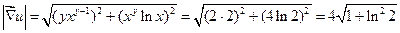ПРИМЕР.Найдите нормаль к поверхности 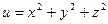в точке Р (1,1,1).

Решение: По свойству 3 , , = .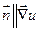

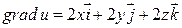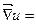
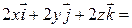
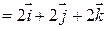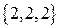
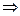
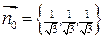ПРИМЕР.Найдите градиент функции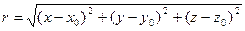
(модуль радиус-вектора).

Решение:

P ₀ -фиксированная точка, P (x, y, z) – изучаемая точка поверхности.

= =

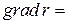
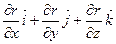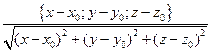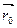
- единичный вектор направления вектора P ₀ P.

Например, покажем, что для 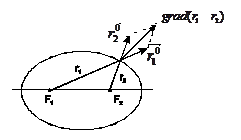скалярной функции 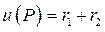, где 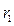, 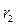- расстояния от точки Р до фиксированных точек 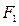, , 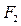линиями уровня являются эллипсы.

Решение:

Имеем: 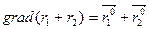, т.е. градиент равен диагонали ромба, построенного на ортах радиус-векторов, проведенных к точке Р из фокусов 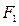и 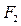. Нормаль к эллипсу в какой-либо точке делит пополам угол между радиус-векторами, проведёнными в эту точку.

Физическая интерпретация: луч света, вышедший из одного фокуса, попадает в другой фокус.