 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Замена перемен. в опред.И.Интегрир.по частям
|
|
Пусть ф-ция х=φ(t)определена,непрерывна,дифиринцирована,монотонна на отр.[α;β]. φ(α)=а,φ(β)=в. f(х)непрерывна на отр.[а;в],тогда  =
=  ∙φ،(t)dt. Если ф-цииu=u(x) и v=v(x)- непрерывно дифференцируемые на отр.[а;в] ф-ции,то имеет место формула интегрирования по частям в опред.И
∙φ،(t)dt. Если ф-цииu=u(x) и v=v(x)- непрерывно дифференцируемые на отр.[а;в] ф-ции,то имеет место формула интегрирования по частям в опред.И  =uv│ва-
=uv│ва-  .Найдём И
.Найдём И  методом интегрирования по частям.
методом интегрирования по частям.  =х
=х  -
-  =-
=-  =-
=-  +4
+4  =(*)
=(*)
 =4arcsin
=4arcsin  =
=  ;
;  =
= 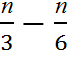 ; (*)=-
; (*)=-  -
-  =
= 
Дата публикования: 2014-11-04; Прочитано: 376 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
