Двуполостной гипрболоид

Двуполостным гиперболоидом называется поверхность, заданная уравнением

(57)

Рассмотрим сечения горизонтальными плоскостями 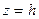, где 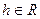. В сечениях образуются линии

(1)

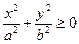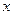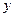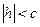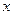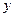Так как при любых значениях и , то при первое уравнение не выполняется ни при каких и . Следовательно, плоскости 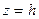, где 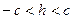, не пересекают данную поверхность.

Если 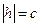, то Û . Следовательно, в сечениях плоскостями и образуется пара точек с координатам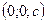и и .

Если , то . Следовательно, первое уравнение из (1) можно записать в форме

, где . (2)

Уравнение (2) является уравнением эллипса с полуосям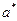и и 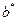. Заметим, что при увеличении 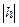от значения 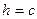до бесконечночти полуоси эллипса 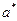и 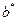так же неограниченно увеличиваются. Итак, при 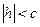плоскости 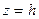не пересекают поверхность, при 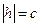в сечениях образуются точки, при в сечениях образуются эллипсы.

Пусть 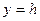, где 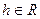. Тогда в сечениях образуются линии

(1)

Следовательно, на плоскости 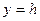при любых значениях , образуется гипербола

, где , (2)

с действительной полуосью и мнимой - 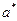, оринтированная вдоль оси .

	Рис.35

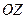В сечениях вертикальными плоскостями , где 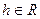, также образуются гиперболы, ориентированные вдоль оси 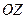(исследовать самостоятельно).

Итак, в сечениях вертикальными плоскостями и при любых значениях образуются гиперболы, в сечениях горизонтальными плоскостям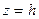и при образуются либо точки, либо эллипсы (рис.35).

В заключении отметим, что уравнения (52)-(57) яляются частными случаями алгебраического уравнения (51). Следовательно, рассмотренные поверхности являются разновидностями поверхностей второго пордка.