 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Цилиндрические поверхнсоти
|
|
Поверхность, образованная всеми прямыми, проходящими параллельно данной прямой 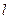 через точки линии
через точки линии  , называется цилиндрической поверхностью (рис.29).
, называется цилиндрической поверхностью (рис.29).

|
При этом линия  называется направляющей, а прямые, проходящие через точки кривой
называется направляющей, а прямые, проходящие через точки кривой  параллельно прямой
параллельно прямой 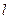 , называются ее образующими.
, называются ее образующими.
Пусть на плоскости 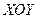 дана своим уравнением
дана своим уравнением  некоторая линия
некоторая линия  (рис.30).
(рис.30).
|
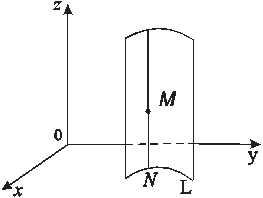
Проведем через каждую точку кривой  прямую параллельно оси
прямую параллельно оси 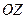 . Тогда получим цилиндрическую поверхность с образующими, парллельными этой оси. Докажем, что уравнение
. Тогда получим цилиндрическую поверхность с образующими, парллельными этой оси. Докажем, что уравнение
 (53)
(53)
будет уравнением этой плоскости.
Выберем на кривой  произвольную точку
произвольную точку 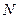 и проведем через нее образующую парллельно оси
и проведем через нее образующую парллельно оси 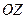 . Выберем на этой образующей произвольную точку
. Выберем на этой образующей произвольную точку 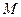 (рис.30). Тогда точки
(рис.30). Тогда точки 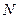 и
и 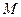 будут иметь одни и те же координтаы
будут иметь одни и те же координтаы 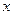 и
и 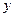 . Следовательно, уравнению (53), не содержащему переменную
. Следовательно, уравнению (53), не содержащему переменную 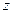 , будут удовлетворять координаты обеих точек. А это значит, что уравнение
, будут удовлетворять координаты обеих точек. А это значит, что уравнение  , не содержащее переменной
, не содержащее переменной 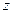 , является уравнением цилиндрической поверхности с образующими, параллельными оси
, является уравнением цилиндрической поверхности с образующими, параллельными оси 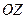 . Аналогично доказывается, что уравнения
. Аналогично доказывается, что уравнения  и
и  , не содержащие переменные
, не содержащие переменные 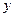 и
и 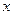 соответственно, определяют цилиндрические поверхности с образующими, парллельными осям
соответственно, определяют цилиндрические поверхности с образующими, парллельными осям 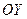 и
и 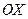 соответственно. Следовательно, и алгебраичесике уравнения (51), не содержащие по одной из переменных, определяют цилиндрические поверхности, образующие которых направлены вдоль соответстующих осей координат. Например, уравнение
соответственно. Следовательно, и алгебраичесике уравнения (51), не содержащие по одной из переменных, определяют цилиндрические поверхности, образующие которых направлены вдоль соответстующих осей координат. Например, уравнение 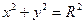 в пространстве трех переменных определяет круговой цилиндр с образующими, парллельными оси
в пространстве трех переменных определяет круговой цилиндр с образующими, парллельными оси 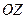 .
.

|
Заметим, что название цилиндрической поверхности определяется названием направляющей. Например, если направляющая  дана уравнением
дана уравнением  , то кривая
, то кривая  является параболой с осью симметрии
является параболой с осью симметрии 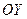 . Тогда это же уравнение в пространстве
. Тогда это же уравнение в пространстве  определяет параболический цилиндр с образующими, парллельными оси
определяет параболический цилиндр с образующими, парллельными оси 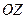 (рис.31).
(рис.31).
Аналогично уравнение  определяет эллиптический цилиндр с образующими, параллельными оси
определяет эллиптический цилиндр с образующими, параллельными оси 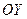 , а уравнение
, а уравнение  определяет гиперболический цилиндр с образующими, параллельными оси
определяет гиперболический цилиндр с образующими, параллельными оси 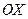 .
.
Дата публикования: 2014-11-04; Прочитано: 271 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
