Угол между двумя прямыми

Пусть в пространстве даны две прямые

.

Рис.26

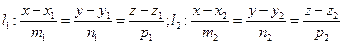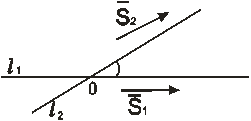
Под углом между двумя прямыми в пространстве понимают любой из углов, образованных двумя прямыми, проведенными из одной точки параллельно данными прямым (рис.26). Обозначим угол между направляющими векторам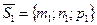и и 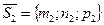данных прямых через 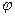. Тогда один из смежных углов между прямым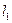и и 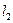также равен 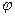. Следовательно,

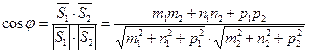. (45)

Заметим, что если 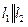, то векторы 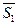, 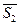коллинеарны. Тогда

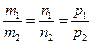. (46)

Условия (46) называются условием параллельрности двух прямых в пространстве .

Если же 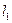^ 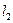, то и 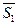^ 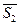. Тогда .

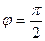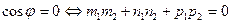. (47)

Условие (47) называется условием перпендикулярности двух прямых в пространстве .

ПРИМЕР 23.1. Найти уравнения прямой, проходящей через точку 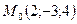перпендикулярно двум прямым 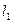и .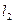

.

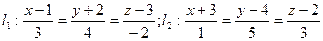Решение. Так ка искомая прямая проходит через данную точку 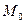, то ее уравнения будем искать в ви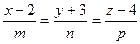де , где ее неизвестный направляющий вектор.

По условию искомая прямая перпендикулярна прямым 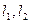. Тогда 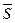^ 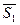, 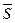^ 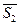, где 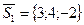, 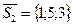есть направляющие векторы векторы данных прямых. Следовательно, за направляющий вектор 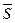можно принять вектор .

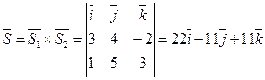Тогда 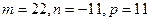, а уравнениями искомой прямой являются уравнения

.

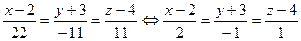24. Прямая и плоскость в пространстве .

Пусть дана в пространстве даны своими уравнениями прямая 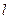и плоскость :

, .

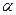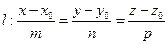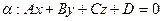Для определения взаимного расположения прямой и плоскости в пространстве достаточно установить, параллельна ли прямая 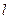плоскости 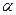или нет. Если нет, то в какой точке ее пересекает и под каким углом.