 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Эллиптический параболоид
|
|
Пусть задано уравнение 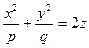 , где
, где 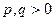 , (55)
, (55)
Являющееся частным случаем уравнения (51). Изучим вид поверхности, соответствующий уравнению (55), методом сечений.
Рассмотрим сечения поверхности горизонтальными плоскостями 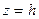 , где
, где 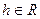 . В сечении, в общем случае, получим линию:
. В сечении, в общем случае, получим линию:
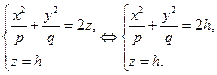 (1)
(1)
Так как по условию 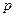 и
и 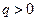 , то
, то 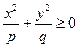 при любых значениях
при любых значениях 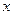 и
и 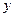 . Следовательно, при
. Следовательно, при 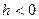 горизонтальные плоскости
горизонтальные плоскости 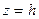 не пересекают поверхность. При
не пересекают поверхность. При 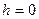 , т.е. на плоскости
, т.е. на плоскости 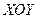 , получим точку
, получим точку 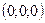 . При
. При 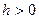 на плоскости
на плоскости 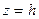 получим линию
получим линию

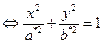 , (2)
, (2)
где 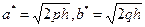 .
.
Уравнение (2) на плоскости  определяет эллипс с полуосями
определяет эллипс с полуосями 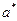 и
и 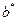 . Следовательно, в сечениях горизонтальными плоскостями
. Следовательно, в сечениях горизонтальными плоскостями 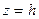 , где
, где 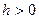 , образуются эллипсы с полуосями
, образуются эллипсы с полуосями 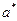 и
и 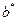 . Заметим, что при увеличении
. Заметим, что при увеличении  от 0 до
от 0 до 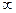 полуоси эллипса неограниченно увеличиваются.
полуоси эллипса неограниченно увеличиваются.
Рассмотрим сечение вертикальной плоскостью 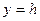 , где
, где 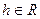 . В сечении получим линию:
. В сечении получим линию:
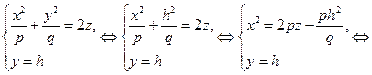
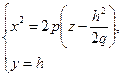 (3)
(3)
Уравнение 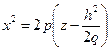 на плоскости
на плоскости 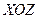 определяет параболу с осью симметрии
определяет параболу с осью симметрии 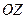 , параметром
, параметром 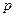 и вершиной, нанаходящейся в точке
и вершиной, нанаходящейся в точке 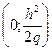 . Следовательно, на плоскости
. Следовательно, на плоскости 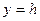 при любых занчениях
при любых занчениях  также получим параболу с параметром, равным
также получим параболу с параметром, равным 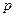 , вершина которой находится в точке
, вершина которой находится в точке 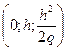 . Заметим, что при увеличении
. Заметим, что при увеличении  от 0 до
от 0 до 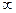 вершина параболы неограниченно поднимается над плоскостью
вершина параболы неограниченно поднимается над плоскостью 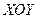 .
.
Итак, в сечениях вертикальными плоскостями 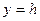 при любых значения
при любых значения  образуются параболы.
образуются параболы.
Аналогичные параболы образуются в сечениях плоскостями 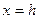 (доказать самостоятельно).
(доказать самостоятельно).
|
Так как в сечениях вертикальными плоскостями 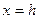 и
и 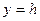 образуются параболы, а в сечениях горизонтальными плоскостями
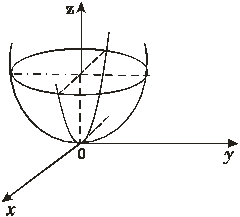
образуются параболы, а в сечениях горизонтальными плоскостями 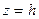 образуются эллипсы, то поверхность (рис.33), определяемая уравнением (55), названа эллиптическим параболоидом.
образуются эллипсы, то поверхность (рис.33), определяемая уравнением (55), названа эллиптическим параболоидом.
Заметим, что если в уравнении (55) 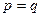 , то в сечениях горизонтальными плоскостями образуются окружности. Следовательно, уравнение
, то в сечениях горизонтальными плоскостями образуются окружности. Следовательно, уравнение 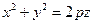 определяет парболоид вращения с осью симметрии
определяет парболоид вращения с осью симметрии 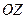 .
.
Дата публикования: 2014-11-04; Прочитано: 401 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
