Точка пересечения прямой с плоскостью

Пусть прямая 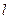пересекает плоскость 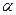в некоторой точке 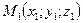. Тогда для определения координат этой точки достаточно решить систему уравнений

(1)

Проще всего решить эту систему, переходя от канонической формы задания уравнения прямой к ее заданию в параметрической форме, т.е. к форме

(2)

где 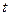- параметр.

Подставляя вместо 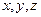их выражения из (2) в первое уравнение системы (1) для определения значения параметра 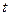для точки пересечения, получим

. (3)

Так как по условию прямая переекает плоскость, то . Следовательно, значение параметра 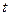для точки пересечения найдется по формуле

. (4)

Подставляя найденное по (4) значение 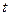в каждое из уравнений (2), вычислим координаты искомой точки .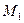

ПРИМЕР 24.1. Найти проекцию точки на плоскость .

Решение. Проведем через точку 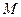прямую 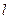перпендикулярно заданной плоскости (рис.28). Уравнения этой прямой будем искать в форме

. (5)

Из условия (49) перпендикулярности прямой и плоскости при получим, что 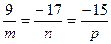. Тогда за проекции направляющего вектора 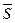прямой 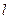можно принять числа .

	Рис.28

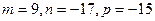Подставляя их в уравнения (5), найдем уравнения перпендикулярна :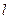

. (6)

Запишем уравнение прямой (6) в параметрической форме:

(7)

Вычислим значения параметра 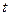для точки пересечения прямой с плоскостю по формуле (4):

.

Подставляя значение в уравнение (7), найдем координаты искомой точки :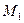

.

Ответ: .