|
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Угол между плоскостями
|
|
Пусть в  заданы своими уравнениями две плоскости
заданы своими уравнениями две плоскости
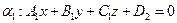 и
и 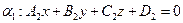 .
.
Коэффициенты 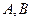 и
и 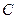 уравнения плоскости являются проекциями нормального вектора
уравнения плоскости являются проекциями нормального вектора 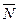 к этой плоскости. Следовательно, один из смежных двугранных углов
к этой плоскости. Следовательно, один из смежных двугранных углов 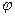 между плоскостями
между плоскостями 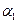 и
и 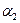 равен углу между нормальными к этим плоскостям векторами:
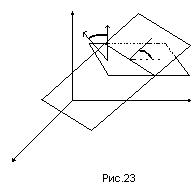
равен углу между нормальными к этим плоскостям векторами:
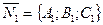 и
и 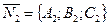 (рис.23).
(рис.23).
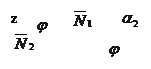 | |||
| |||
| |||||
|
Тогда
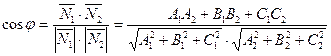 . (37)
. (37)
По формуле (37) определяется один из смежных углов между данными плоскостями.
Следствие 1. Если плоскости 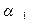 и
и 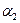 параллельны, то их нормальные векторы
параллельны, то их нормальные векторы 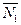 и
и 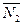 коллинеарны. Тогда
коллинеарны. Тогда
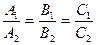 . (38)
. (38)
Условия (38) называются условиями параллельности двух плоскостей.
Следствие 2. Если плоскости 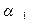 и
и 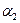 перпендикулярны, то в (37) угол
перпендикулярны, то в (37) угол 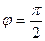 . Тогда
. Тогда 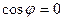 . Следовательно, и
. Следовательно, и
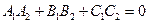 . (39)
. (39)
Условие (39) называется условием перпендикулярности двух плоскостей.
ПРИМЕР 19.1. Определить, при каком значении 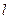 плоскость
плоскость 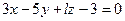 перпендикулярна плоскости
перпендикулярна плоскости 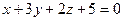 .
.
Решение. Векторы 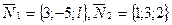 являются нормальныи векторами к данным плоскостям.тогда согласно условию (39) плоскости взаимно перпендикулярны, если
являются нормальныи векторами к данным плоскостям.тогда согласно условию (39) плоскости взаимно перпендикулярны, если 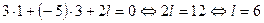 .
.
Ответ: 6.
ПРИМЕР 19.2. Составить уравнение плоскости, которая проходит через точку 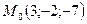 параллельно плоскости
параллельно плоскости 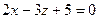 .
.
Решение. Искомая плоскость проходит через заданную точку 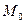 , тогда ее уравнение, согласно формуле (34), запишется в виде
, тогда ее уравнение, согласно формуле (34), запишется в виде
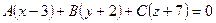 .
.
Искомая плоскость параллельна заданной плоскости. Тогда из условия параллельности двух плоскостей (38) получим
 . Отсюда
. Отсюда 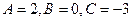 .
.
Подставляя найденные коэффициенты 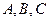 в предыдущее уравнение, найдем уравнение искомой плоскости
в предыдущее уравнение, найдем уравнение искомой плоскости
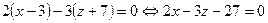 .
.
20. Прямая в пространстве  . Векторное, канонические и параметрические уравнения прямой.
. Векторное, канонические и параметрические уравнения прямой.
Положение прямой 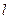 в пространстве
в пространстве  может быть определено заданием:
может быть определено заданием:
1) любых двух точек;
2) ее точки и вектора 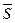 , параллельного этой прямой;
, параллельного этой прямой;
3) 0
Поставим задачу определения уравнения прямой в каждом из этих случаев.
Пусть в пространстве  дана точка
дана точка 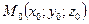 и вектор
и вектор  . Тогда через точку
. Тогда через точку 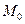 параллельно вектору
параллельно вектору 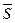 проходит единственная прямая
проходит единственная прямая 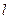 . Для определения ее уравнения выберем в
. Для определения ее уравнения выберем в  произвольную точку
произвольную точку 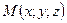 и построим векторы
и построим векторы
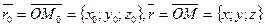 .
.
|  |
| |||||
 | |||
 | |||
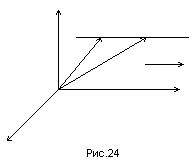
Согласно определению суммы векторов получим
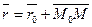 (рис.24).
(рис.24).
Пусть точка 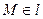 , тогда векторы
, тогда векторы 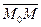 и
и 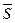 коллинеарны. Следовательно,
коллинеарны. Следовательно, 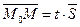 , где
, где 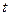 - параметр, принимающий любое значение из
- параметр, принимающий любое значение из 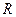 в зависимости от положения точки
в зависимости от положения точки 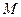 на прямой
на прямой 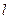 . Тогда для точки
. Тогда для точки 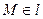 имеем
имеем
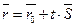 , где
, где 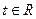 . (40)
. (40)
Если точка 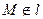 , то векторы
, то векторы 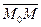 и
и 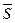 не коллинеарны.
не коллинеарны.
Следовательно, для таких точек равенство (40) не выполняется ни при каких 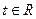 . Итак, уравнение (40) является векторным уравнением прямой, а вектор
. Итак, уравнение (40) является векторным уравнением прямой, а вектор  называется направляющим вектором прямой. Воспользовавшись координатами векторов
называется направляющим вектором прямой. Воспользовавшись координатами векторов 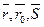 из (40), получим
из (40), получим
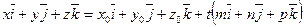 Û
Û
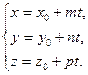 (41)
(41)
Уравнения (41) называются параметрическими уравнениями прямой 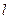 с параметром
с параметром 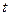 в пространстве
в пространстве  .
.
Исключая параметр 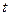 из уравнений (41), найдем, что
из уравнений (41), найдем, что
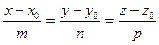 . (42)
. (42)
Уравнения (42) называются каноническими уравнениями прямой 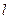 в пространстве
в пространстве  .
.
Замечание. В уравнении (42) условились считать, что числа 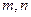 и
и 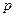 могут принимать любые значения, кроме одновременного равенства
могут принимать любые значения, кроме одновременного равенства 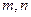 и
и 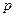 нулю. В частности, если уравнение (423) имеет вид
нулю. В частности, если уравнение (423) имеет вид 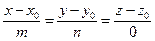 , о это уравнение есть уравнение прямой, перпендикулярной оси
, о это уравнение есть уравнение прямой, перпендикулярной оси 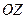 . Действительно, при
. Действительно, при 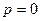 направляющий вектор
направляющий вектор 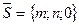 перпендикулярен оси
перпендикулярен оси 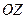 . Следовательно, и параллельная вектору
. Следовательно, и параллельная вектору 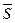 прямая перпендикулярна этой оси. Если же уравнение (42) имеет вид
прямая перпендикулярна этой оси. Если же уравнение (42) имеет вид 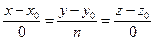 ,то это уравнение является уравнением прямой, перпендикулярной плоскости.
,то это уравнение является уравнением прямой, перпендикулярной плоскости.
ПРИМЕР 20.1. Определить, лежит ли точка 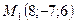 на прямой
на прямой 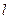 , проходящей через точку
, проходящей через точку 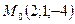 параллельно вектору
параллельно вектору 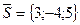 .
.
Решение. Найдем уравнения прямой 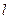 в канонической форме. Полагая
в канонической форме. Полагая 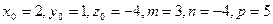 , получим
, получим 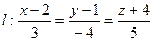 .
.
Подставляя в эти уравнения координаты точки 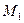 , найдем
, найдем 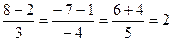 .
.
Следовательно, точка 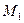 принадлежит прямой
принадлежит прямой 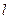 .
.
Дата публикования: 2014-11-04; Прочитано: 374 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!