 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Уравнение плоскости по трем точкам
|
|
Пусть в пространстве 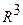 даны три точки
даны три точки  ,
,  ,
,  , не лежащие на одной прямой. Выберем в этом пространстве произвольную точку
, не лежащие на одной прямой. Выберем в этом пространстве произвольную точку 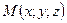 и построим три вектора
и построим три вектора  ,
,  ,
,  .
.
| |||
 | |||

 | |||
|
Предположим, что точка 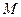 лежит на плоскости
лежит на плоскости 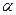 (рис.22), проходящей через заданные точки
(рис.22), проходящей через заданные точки 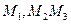 . Тогда векторы
. Тогда векторы 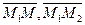 и
и 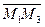 лежат на этой плоскости. Следовательно,
лежат на этой плоскости. Следовательно,  Û
Û
 . (35)
. (35)
Если же точка  , то векторы
, то векторы 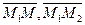 и
и 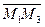 некомпланарны. Тогда и их смешанное произведение отлично от нуля. Согласно определению 15.1 уравнение (35) является уравнением искомой плоскости
некомпланарны. Тогда и их смешанное произведение отлично от нуля. Согласно определению 15.1 уравнение (35) является уравнением искомой плоскости 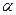 .
.
Заметим, что если расписать определитель (35), то полученное уравнение так же, как и уравнение (34), будет алгебраическим уравнением первой степени относительно трех переменных 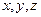 .
.
Дата публикования: 2014-11-04; Прочитано: 342 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
