 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Секвенциально непрерывные отображения топологических пространств
|
|
Связь между непрерывностью и секвенциальной непрерывностью
Опр. Пусть X,Y –Т.П. Отображение f:X->Y наз секвенциально непрерывным, если ᗄx  X и ᗄ посл.
X и ᗄ посл.
 точек пр-ва X из Xn->X=> f(xn)->f(x)
точек пр-ва X из Xn->X=> f(xn)->f(x)

Утв. Пусть X,Y-Т.П. f:X->Y – отображения.
а) Если f непр., то f секв. непр.
б) Если X метризуемо и f секв. непр., то f-непр.
Док-во
а) Пусть f-непр => f-cекв. непр.
Пусть в X xn->x Покажем, что f(xn)->f(x) (в Y)

Ǝ окр V т-ки x | f(V) ⊆U
Ǝ p 
 | ᗄn
| ᗄn  p xn
p xn  V
V
Тогда ᗄn  p f(xn)
p f(xn)  U, т.е. f(xn) ->f(x)
U, т.е. f(xn) ->f(x)
б) Пусть ρ-метрика согласованна с топологией пр-ва X От противного

Допустим Ǝ x  X | f – разр. в т. x, т.е. Ǝ окр U т-ки f(x) | ᗄокр V т-ки x вып. f(V) ⊈ U.
X | f – разр. в т. x, т.е. Ǝ окр U т-ки f(x) | ᗄокр V т-ки x вып. f(V) ⊈ U.
В частности, ᗄn  Ǝ x1
Ǝ x1  Bp(x,
Bp(x,  )| f(xn) ⊈ U. Тогда xn->x, но f(xn) не -> f(x)
)| f(xn) ⊈ U. Тогда xn->x, но f(xn) не -> f(x) 
21.Понятие гомеоморфизма. Пример: стереографическая проекция. Пример непрерывной биекции, не являющейся гомеоморфизмом

Опр. Пусть X, Y – Т.П. Отображение f: X → Y Называется гомеоморфизмом, если:
1) f-биекция
2) f-непр.
3) f-1: Y→X-непр
Если Ǝ гомеоморфизм f: X → Y то пр-ва X и Y называются гомеоморфными (X≈Y)
Замечание 1. Если X-ТП- гомеоморфно подпр-ву В пр-ва Y, то говорим что X гомеоморфно вкладывается в Y, а гомеоморфизм f:X→В наз. Гомеоморфным вложением пр-ва X в пр-во Y (X  Y).
Y).

Замечание 2.
Пусть X, Y, Z – Т.П.
1)X≈X; id: X →X.
2)Если У≈X,то и X≈Y.
3)Если X≈Y, Y≈Z, то и X≈Z.
Замечание 3.
Любая изометрия метрических пространств явл. гомеоморфизмом.

Примеры: 1) Пусть f: Rn→R- аф. преобр.  непр.
непр.

f- непр. f-1- аф. пр-е => f-1 непр. f- гомеоморфно
Аф. Экв. Фигуры- гомеоморфны.
2)Любой интервал ]a, в[⊆ℝ гомеоморфен ℝ
а в R ]a, в[ ≈]0;1[
ϕ: ]0,1[→]а,b[: t →a + t(b-а)
Пок. что  ≈ℝ
≈ℝ

f:  →ℝ; f(t)=tg t
→ℝ; f(t)=tg t
3)Любой шар пр-ва ℝn гомеоморфен ℝn Ǝ аф. преобразование, которое Bn(a,r) перев. В шар Bn с ц. в.т. о рад 1


Bn≈ℝn; f:Bn->ℝn:x.-> 
f-непр.;  =(x1,…,xn); f(
=(x1,…,xn); f( )=(
)=( -непр, f-инъективно, пусть
-непр, f-инъективно, пусть 
 ⟹
⟹ 
f-cюръективно, рассмотрим  ℝn, ищем x. | f(
ℝn, ищем x. | f( )=
)= 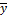 .
.
 ищем в виде
ищем в виде  , 𝜆>0
, 𝜆>0
 , (
, (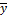 ≠0, 𝜆>0)=>
≠0, 𝜆>0)=>  =1
=1
𝜆=1-𝜆|| 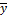 ||, α=
||, α= 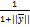 ; x.=
; x.=  кончим прообраз. f-1-непрерывно.
кончим прообраз. f-1-непрерывно.
4) Пусть M⊆ ℝ; p:M->ℝ непр. отобр.

Рассмотрим на пл-ти ℝ2 фигуру Гf:y=f(x) покажем, что Гf≈M h:M->Гf; h(t)=(t,f(t)) h-гомеоморфно
4I) На пл-ти ℝ2 рассмотрим фигуру Ф:y=x2
f:ℝ->ℝ; f(x)=x2; Ф≈ℝ

парабола гомеоморфна прямой
Рассмотрим  : xy=1
: xy=1
x>0
f.:]0, + 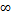 [->ℝ
[->ℝ  график
график  .
.
 (x)=
(x)=  ; ]0,+
; ]0,+ 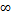 [≈ Ф.
[≈ Ф.

Заметим: ]0;+ 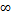 [≈ℝ
[≈ℝ
Гомеоморфизм g:]0;+ 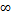 [≈ℝ задается формулой g(x)=Ln x; Ф. ≈ℝ.
[≈ℝ задается формулой g(x)=Ln x; Ф. ≈ℝ.
Ветвь гиперболы ≈ℝ
Парабола ≈ ветви гиперболы

5) Пусть M⊆ℝ2; f:M->ℝ непр. отобр. Рассмотрим в ℝ3 фигуру Гf зад ур-ем z=f(x,y)
Гf≈М
h:M->Гf
h(x,y)=(x,y,f(x,y))
h – гомеоморфизм

5’) В ℝ3 рассмотрим фигуру Ф: x2+y2-z2=-1
z  0
0

Фóz= 
Ф-гр. отобр f:ℝ2->ℝ опр. по правилу f(x,y)= 
Ф≈ℝ2
Дата публикования: 2015-11-01; Прочитано: 1270 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
