Пример решения работы. Задание №10.Найти пределы функций, не пользуясь правилом Лопиталя: а) ; б) ; в)

Задание №10. Найти пределы функций, не пользуясь правилом Лопиталя:

а) ;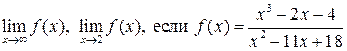
б) 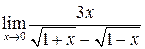;	в) 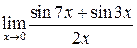;	г) .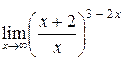

Решение

а) Предел 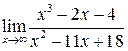содержит неопределенность 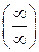. Для того, чтобы раскрыть эту неопределенность, следует разделить числитель и знаменатель на 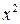− значение переменной в наибольшей степени знаменателя. Тогда

.

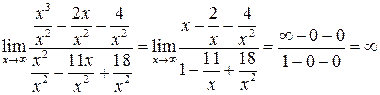Предел 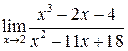содержит неопределенность 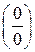. Для того, чтобы раскрыть эту неопределенность, следует преобразовать числитель и знаменатель, разложив их на множители. Разделим числитель и знаменатель на 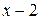, то есть на тот множитель, который обращает их в 0.

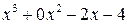
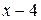
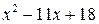
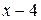
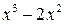
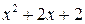
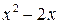
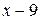
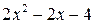
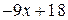
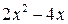
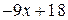
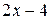
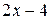
Тогда:

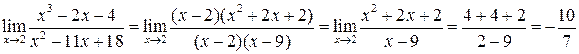
б) Предел 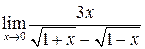содержит неопределенность вида 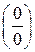. Для этого, чтобы раскрыть эту неопределенность, следует знаменатель и числитель умножить на сопряженный многочлен знаменателя :

.

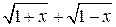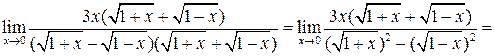
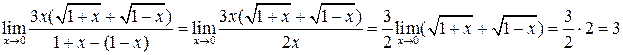в) Предел 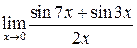содержит неопределенность вида 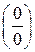. Для раскрытия этой неопределенности преобразуем сумму синусов, стоящих в числителе, в произведение:

,

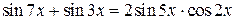получим

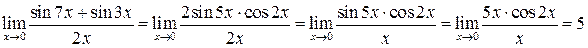
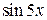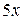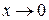(заменим на эквивалентную бесконечно малую при , а ).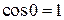

г) При вычислении предела 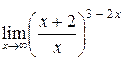имеем дело с неопределенностью (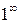). Преобразуем выражение в скобках, выделим 1 и бесконечно малую функцию:

.

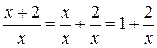Итак,

.

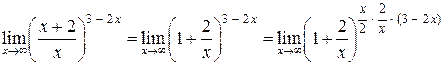Так как при 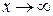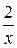− бесконечно малая величина, то .

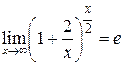Поскольку 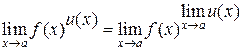, получаем:

.

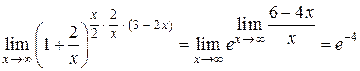Ответ: а) 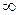; ; 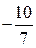б) 3; в) 5; г) .

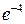Задание №11. Задана функция 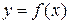. Найти точки разрыва функции, если они существуют. Сделать чертеж.

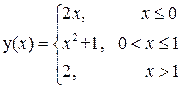
Решение

Очевидно, исследованию подлежат точк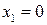и и 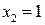, так как в остальных точках числовой оси данная функция 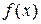непрерывна (представлена непрерывными на всей числовой оси функциям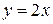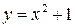и , и .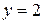

1) 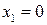. Найдем односторонние пределы:

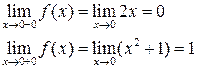
Так как предел функции слева не равен пределу справа, но эти пределы конечны, то в точке 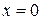данная функция терпит разрыв I рода.

2)

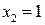
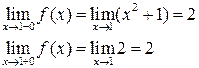
Так как 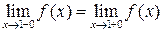, то 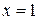− точка непрерывности данной функции .

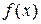График функции представлен на рисунке.

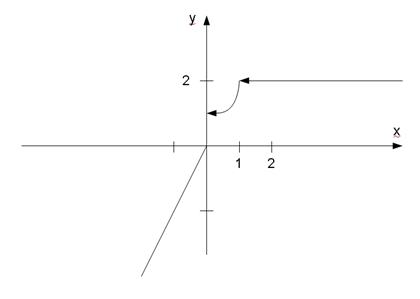
Задание №12. а) Дана функция 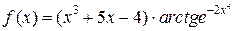. Найти .

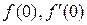б) Найти производные 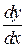данных функций:

1) ;

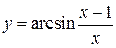2) ;

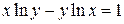3) .

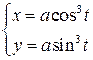Решение

а) Очевидно, что .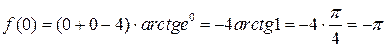

Чтобы найти 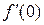найдем сначала 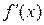. По правилу дифференцирования произведения двух функций и по правилу дифференцирования сложной функции имеем:

.

.

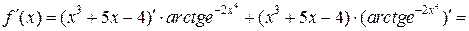
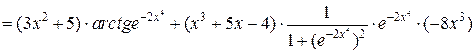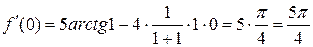б) 1) .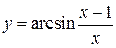

По правилу дифференцирования сложной функции:

.

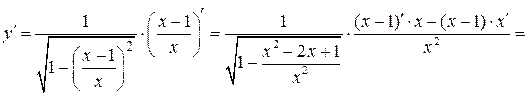
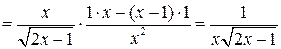2)

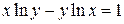
Это неявно заданная функция. Найдем производные обеих частей данного равенства. Не забудем при этом, что .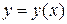

.

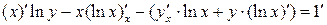
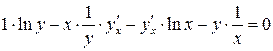
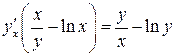
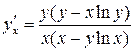3)

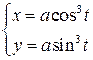
В этом случае функция задана параметрическим способом. Производная от такой функции находится по формуле:

.

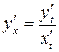Найдем 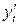и :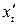

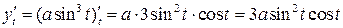
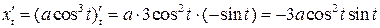
Но тогда

.

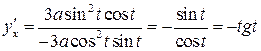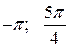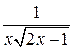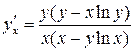Ответ: а) . б) 1) ; 2) ; 3) .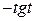

Задание №13. Показать, что функция 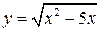удовлетворяет уравнению

.

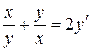Решение

Найдем :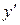

.

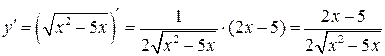Левая часть данного уравнения при 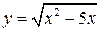примет вид:

;

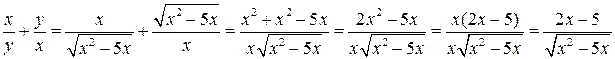Правая часть:

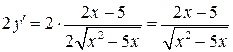, что и требовалось установить.