Упражнение 11. Свойства суммы векторов

Проверить свойства суммы векторов, используя векторы

a=(2;3;4), b=(3;5;2),c=(1;1;1),

сначала непосредственно, затем используя функцию isequal(,).

Сделать геометрическую интерпретацию.

Произведением вектора 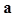на число 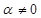назовем вектор 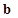, удовлетворяющий следующим трем условиям:

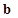· коллинеарен ;

· ;

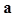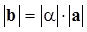· направление 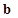совпадает с направлением 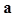, если 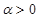, и противоположно ему, если .

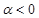Обозначение: .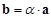

Под произведением вектора 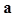на число 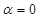будем понимать нулевой вектор θ. Напомним, нулевой вектор, в силу его определения, не имеет направления, а длина его равна нулю.

Вектор имеет длину такую же, как вектор 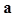(уметь доказывать),
и направление, противоположное направлению 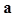(так как число (– 1) < 0).

Вектор 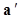называется противоположным для вектора .

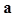Свойства умножения вектора на число:

1) 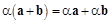– распределительное или дистрибутивное свойство;

2) 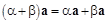– распределительное или дистрибутивное свойство;

3) 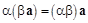– сочетательное или ассоциативное свойство.

(дистрибутивность от латинского distributivus — «распределительный»)