Пример 2. Вычисление скалярного произведения в косоугольном базисе, состоящем из единичных векторов

Пусть p и q – косоугольный базис, векторы длины один,
а угол между ними равен 60^о, a =3 p +4 q, b =2 p - q.
Найти скалярное произведение (a, b), длины векторов a и b..

Решение.

(a, b)=(3 p +4 q,2 p - q)=(3 p,2 p - q)+(4 q,2 p - q)=(3 p,2 p)+(3 p,- q)+(4 q,2 p)+(4 q,- q)=

=6(p, p)-3(p, q)+8(q, p)-4(q, q)=6(p, p)+5(p, q)+4(q, q)=6+5 -4 =6+5/2-4=4,5

если придать вычислениям общий вид: a =a₁ p +a₂ q, b =b₁ p +b₂ q, получим:

* - формула для вычисления скалярного произведения в координатной форме изменилась.

(a, a)=(3 p +4 q, 3 p +4 q)= 9(p, p)+2*12*(p, q)+16(q, q)=9+2*12* +16=37.

.

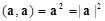- скалярный квадрат по-прежнему равен квадрату длины вектора,

но вычисляются они теперь по-другому.

(b, b)=(2 p - q, 2 p - q)= 4(p, p)-4(p, q)+(q, q)=4-2*2* +1=3.

.

Ответ. (a, b)=3, , .

Пример 3. Вычисление скалярного произведения в косоугольном базисе, состоящем из векторов произвольной длины.

Пусть p и q – косоугольный базис, причем длины векторов равны 2 и 3 соответственно, а угол между ними равен 60^о, a =3 p +4 q, b =2 p - q.
Найти скалярное произведение (a, b), длины векторов a и b..

Решение.

(a, b)=(3 p +4 q,2 p - q)=(3 p,2 p - q)+(4 q,2 p - q)=(3 p,2 p)+(3 p,- q)+(4 q,2 p)+(4 q,- q)=

=6(p, p)-3(p, q)+8(q, p)-4(q, q)=6(p, p)+5(p, q)+4(q, q)=6*2*2+5*2*3* – 4*3*3= =24+15 – 36=3

если придать вычислениям общий вид: a =a₁ p +a₂ q, b =b₁ p +b₂ q, получим:

+ * - формула для вычисления скалярного произведения в координатной форме снова изменилась.

(a, a)=(3 p +4 q, 3 p +4 q)= 9(p, p)+24(p, q)+16(q, q)=

= =

=9*2*2+24*2*3* +16*3*3=252.

.

(b, b)=(2 p - q, 2 p - q)= 4(p, p)-4(p, q)+(q, q)=4*2*2-4*2*3* +3*3=13.

.

Ответ. (a, b)=3, , .

В примерах 1,2 и 3 показано как усложняются расчеты вычисления скалярного произведения векторов и длины вектора в косоугольной системе координат по сравнению с декартовой прямоугольной системой координат.