Работа сил, приложенных к метриальной точке и твердому телу

Работа силы тяжести. Пусть точка М, на которую действует сила тяжести, перемещается из положения в положение (рис. 3.8).

Проекции силы на оси координат равны , , . Используя выражение (3.19), определяем .

Если точка выше , то , где h величина вертикального перемещения точки; если же точка ниже точки , то .

Поэтому можно записать . (3.22)

Следовательно, работа силы тяжести равна произведению модуля силы на вертикальное перемещение точки её приложения, взятое с соответствующим знаком. Если точка перемещается вверх, то знак минус, если вниз то плюс.

Работа силы тяжести не зависит от вида траектории перемещения точки.

Работа силы упругости. Рассмотрим пружину ВС, конец C которой закреплён неподвижно (рис. 3.9). При растяжении пружины возникают силы упругости, и на тело, вызывающее растяжение, действует реакция пружины . Эта сила направлена противоположно перемещению свободного конца пружины, а её модуль пропорционален удлинению пружины: ,

где с  коэффициент жесткости пружины.

Ось x направим по оси пружины, приняв за начало координат конец недеформированной пружины В. Проекция силы на ось х определяется как .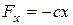

Вычислим работу силы упругости на перемещении, используя понятие элементарной работы (3.19): .

Проекции силы упругости на оси: ; ; ,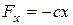

отсюда элементарная работа силы упругости ,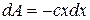

а работа силы упругости на перемещении определяется как (3.23)

Работа силы упругости отрицательна в том случае, когда деформация увеличивается, то есть когда сила упругости направлена противоположно перемещению её точки приложения, и положительна, когда деформация уменьшается.

Работа силы, приложенной к вращающемуся телу. Пусть сила приложена в некоторой точке тела, отстоящей от оси вращения z на величину h (см. рис. 3.10).

Точка приложения силы описывает при своём движении окружность радиуса h. Разложим силу по осям естественного трёхгранника и обозначим её составляющие через . Работа составляющих и равна нулю, так как эти силы перпендикулярны к перемещению точки их приложения. Следовательно, работа силы равна работе eё касательной составляющей.

Для элементарной работы имеем ,

где  дифференциал дуговой координаты точки приложения силы, а  дифференциал угла поворота тела. Учитывая, что произведение равно моменту силы относительно оси вращения тела, получаем . (3.24)

Элементарная работа силы, приложенной к вращающемуся телу, равна моменту этой силы относительно оси вращения, умноженному на дифференциал угла поворота тела. Работа силы на конечном углу поворота определяется как , (3.25)где и  начальное и конечное значение угла поворота тела.

Если момент является постоянной величиной, то есть , то . (3.26)

Делим обе части равенства (3.24) на и получаем выражение для мощности силы, приложенной к вращающемуся телу: , . (3.27)

Мощность силы , приложенной к вращающемуся телу, равна произведению момента этой силы относительно оси вращения на угловую скорость тела.