Эпюры внутренних силовых факторов

Для определения положения наиболее нагруженного сечения стержня при изгибе, как и при других видах нагружения, необходимо иметь эпюры внутренних силовых факторов. Рассмотрим балку на двух опорах (рис. 4.24, а), нагруженную сосредоточенной внешней силой (активной) F. Собственный вес балки учитывать не будем.

Согласно порядку построения эпюры (см. параграф 4.2.1) прежде всего необходимо определить все внешние нагрузки, действующие на стержень.

В сечении А расположена шарнирно-неподвижная опора, создающая в общем случае нагружения две реактивных составляющих RА и НА, а в сечении В имеем шарнирно-подвижную опору, которая создает одну реактивную составляющую RВ. Отмеченные опорные реакции определим из уравнений равновесия балки:

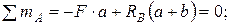
Решая данные уравнения совместно, получаем HA = 0;

Для проверки правильности определения реакций необходимо записать еще одно уравнение равновесия, например

и, подставив в него найденные значения реакций, убедиться в его выполнении.

Следующим этапом построения эпюры является выделение силовых участков (понятие участка приведено в параграфе 4.2.1).

Для исследуемого стержня имеем два силовых участка: АС, СВ. Далее, используя метод сечений (см. параграф 4.1.2), на каждом участке записываем аналитические выражения для внутренних силовых факторов.

На участке АС рассмотрим равновесие мысленно отсеченной части стержня длиной . Эта часть стержня нагружена внешней сосредоточенной силой RA, которую должна уравновесить внутренняя поперечная сила . Если на рассматриваемую часть стержня действует несколько внешних сил, то внутренняя сила будет равна сумме их проекций на ось y.

Следовательно, (4.51)

Примем следующее правило знаков для внутренней поперечной силы. Если внешняя сила направлена таким образом, что стремится повернуть рассматриваемую часть стержня относительно сечения по часовой стрелке, то она создает положительную внутреннюю силу (см. рис. 4.25).

Согласно правилу знаков внешняя сила RA в сечении х 1 создает положительную внутреннюю силу (см. рис. 4.24, б). Однако рассматриваемая часть стержня длиной х 1 под действием RA и в равновесии не находится, так как эти силы создают момент, равный .

Следовательно, в сечении х 1 должен возникать внутренний момент , уравновешивающий момент от силы RA.

Таким образом, если на рассматриваемую часть действует несколько внешних нагрузок, то изгибающий момент в сечении стержня равен сумме моментов от внешних нагрузок, взятых относительно центра тяжести рассматриваемого сечения, то есть момент в сечении х 1 будет равен . (4.52)

Рассмотрим правило знаков для внутреннего момента. Если внешние нагрузки деформируют рассматриваемую часть стержня, мысленно закрепленную в сечении, выпуклостью вниз, то они создают положительный момент (рис. 4.25).

В соответствии с данным правилом внешняя сила RА в сечении х 1 создает положительный внутренний момент (см. рис. 4.24, б), который согласно выражению (4.52) линейно зависит от х 1. Поэтому, чтобы построить эпюру моментов на участке АС, необходимо знать значение момента в начале участка и в конце: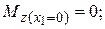

Для участка СВ удобнее начало координат перенести в сечение В и рассмотреть равновесие мысленно отсеченной части стержня длиной х 2 (см. рис. 4.24, а). Тогда для ВС () ; (4.53) (4.54)

Согласно выражениям (4.53) и (4.54) внутренняя поперечная сила на участке ВС  постоянная и отрицательная, а момент  положительный и изменяется по линейному закону.

В начале участка в конце –

По полученным выражениям для внутренних силовых факторов строим эпюру и (см. рис. 4.24, г).

На эпюре в сечении, где приложена сосредоточенная внешняя сила, будет скачок на величину этой силы, а на эпюре  излом. Скачок на эпюре будет иметь место в том сечении, в котором приложен сосредоточенный внешний момент, причем величина скачка равна соответствующему моменту.

Построим эпюры поперечных сил и изгибающих моментов для балки, нагруженной равномерно распределенной нагрузкой q (рис. 4.26).

Опорные реакции для данного примера могут быть определены и без записи условий равновесия, так как система симметрична, значит каждая опора берет на себя половину активной нагрузки: Балка имеет один силовой участок АВ Начало координат расположим в опоре А.

Мысленно сделаем сечение на расстоянии х от опоры А и рассмотрим равновесие этой части стержня.

При этом получим (4.55)

(4.56)

Уравнение (4.55) является уравнением прямой линии, для построения которой достаточно два значения:

Эпюра поперечных сил представлена на рис. 4.26, б.

Уравнение (4.56) соответствует параболе.

Для ее построения необходимо знать положение экстремума и его значение. Положение экстремума функции определим, приравняв ее первую производную к нулю: 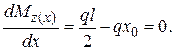(4.57)

Тогда из (4.57) можно найти значение координаты при котором изгибающий момент принимает экстремальное значение:

Кроме того, найдем значение момента в начале и в конце участка:

Эпюра изгибающих моментов представлена на рис. 4.26, в.

Сопоставляя эпюры и , делаем вывод, что при действии распределенной нагрузки поперечная сила на участке изменяется по линейному закону, а изгибающий момент  по параболическому, причем выпуклость параболы направлена навстречу распределенной нагрузке. Соответственно, в том сечении, где поперечная сила равна нулю, изгибающий момент принимает экстремальное значение – значит, между выражениями для поперечной силы и изгибающего момента существует дифференциальная зависимость.

Рассмотрим это подробнее. Для этого мысленно вырежем из стержня (см. рис. 4.26, а) элемент длиной dx (рис. 4.27). Тогда в левом сечении будут действовать силовые факторы и , а в правом  и .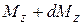

Составим условие равновесия выделенного элемента:

Пренебрегая произведениями и как величинами второго порядка малости по сравнению с остальными слагаемыми, получаем . (4.58)

Дифференциальная зависимость (4.58) используется для определения положения экстремума на эпюре изгибающих моментов, что и было проиллюстрировано выше (выражение 4.57).