Решения избранных задач 3 страница

Рис. О 1	Рис. О 2	Рис. О 3

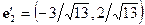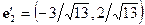4) пересекающиеся прямые , ; 5) параллельные прямые , ; 6) эллипс , , , ; 7) гипербола , , , ; 8) парабола , , , ; 9) пересекающиеся прямые , ; 10) параллельные прямые , ; 11) эллипс , , , ; 12) гипербола , , , ; 13) парабола , , , ; 14) пересекающиеся прямые , ; 15) параллельные прямые , ; 16) эллипс , , , ; 17) гипербола , , , ; 18) парабола , , , ; 19) пересекающиеся прямые , ; 20) параллельные прямые , . 16.4. При
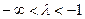– гипербола , действительная ось которой имеет угловой коэффициент, равный –1; при – две параллельные прямые ; при
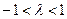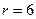– эллипс , большая ось которого имеет угловой коэффициент, равный –1 (при – окружность ); при – две параллельные прямые ; при – гипербола , действительная ось которой имеет угловой коэффициент, равный 1. 16.5. 1) , ; 2) , . 16.6. . 16.7. . 16.8. , . 17.1. 1) , ; 2) , ; 3) , ; 4) , . 17.2. Центр 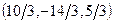, радиус равен 3. 17.3. 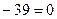. 17.4. . 17.5. . 17.6. ; каноническое уравнение . 17.7. 1) Пара пересекающихся плоскостей , ; 2) сфера 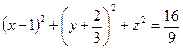; 3) круглый цилиндр ; 4) круглый конус ; 5) пара параллельных плоскостей . 17.8. 1) Эллипсоид ; центр , большая, средняя и малая оси соответственно параллельны осям , , ; 2) однополосный гиперболоид вращения ; центр , ось вращения параллельна оси ; 3) круглый конус ; вершина , ось вращения параллельна оси ; 4) параболоид вращения; , вершина , направляющий вектор оси вращения . 17.9. 1) Круговой цилиндр с радиусом 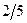; ось цилиндра проходит через точку и имеет направляющий вектор ; 2) параболический цилиндр ; параметр параболы , , являющейся направляющей цилиндра, равен , вершина параболы ; направляющий вектор оси параболы в сторону вогнутости , направляющий вектор образующих цилиндра ; 3) параболический цилиндр ; параметр параболы , равен , вершина параболы 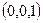; направляющий вектор оси параболы в сторону вогнутости 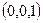, направляющий вектор образующих цилиндра .

ЛИТЕРАТУРА

1. Моденов П. С., Пархоменко А. С. Сборник задач по аналитической геометрии. – М.: Наука, 1976. – 384 с.

2. Немченко К. Э. Аналитическая геометрия. – М.: Эксмо, 2007. – 352 с.

3. Нємченко К. Е. Аналітична геометрія (схеми, таблиці та задачі): Методичні вказівки до курсу «Аналітична геометрія» для студентів першого курсу спеціальностей фізико-математичного напряму. – Харків, 2007.

4. Александров П. С. Лекции по аналитической геометрии. – М.: Наука, 1968.

5. Гельфанд И. М. Лекции по линейной алгебре. – М.: Наука, 1971.

6. Моденов П. С. Аналитическая геометрия. – М.: Изд-во МГУ, 1969.

7. Постников М. М. Аналитическая геометрия. – М.: Наука, 1973.

8. Ильин В. А., Поздняк Э. Г. Аналитическая геометрия: Учебник для вузов. – 5-е изд. – М.: Наука, 1999. – 224 с.

Навчальне видання

Кіценко Юрій Олександрович

Нємченко Костянтин Едуардович

Методичні матеріали з курсу

АНАЛІТИЧНА ГЕОМЕТРІЯ

Оригінал-макет створено на кафедрі теплофізики та молекулярної фізики Фізико-енергетичного факультету Інституту високих технологій

Харківського національного університету імені В. Н. Каразіна

Відповідальний за випуск В. А. Сліпко

Коректор С. В. Гончарук

Комп’ютерна верстка Ю. О. Кіценко

Макет обкладинки

Підписано до друку ___.___.2009. Формат 60х84/18. Ум. друк. арк. 1,2.

Папір друк. офсет. Друк ризо графічний.

Обл. вид. арк. 1,5. Наклад 50 прим. Ціна договірна.

61077, Харків, майдан Свободи, 4, Харківський національний університет імені В. Н. Каразіна, Видавництво ХНУ імені В. Н. Каразіна

Надруковано ХНУ імені В. Н. Каразіна

61077, Харків, майдан Свободи, 4.

Тел. 705-24-32

Свідоцтво про державну реєстрацію ДК №3367 від 13.01.09