Задачи к теме 14

Во всех задачах этой темы система координат – прямоугольная.

14.1(751*). Написать уравнение эллипса, для которого прямые
х + у – 1 = 0 и х – у + 1 = 0 суть соответственно большая и малая оси и длины полуосей которого а = 2, b = 1.

14.2(752*). Написать уравнение параболы, осью которой служит прямая х + у + 1 = 0 и которая проходит через точки (0, 0), (0, 1).

14.3(753*). Написать уравнение гиперболы, зная ее ось 2 х – у + 2 = 0, асимптоту у = 0 и точку (1, 1).

14.4(759). Найти фокусы , и соответствующие им директрисы следующих линий:

1) ; 2) ; 3) .

14.5(760). Найти фокус и директрису параболы

.

14.6(761). Найти фокус F и директрису d параболы .

14.7(762). Найти фокусы и директрисы равносторонней гиперболы .

14.8(763). Написать уравнения эллипса и гиперболы с фокусами (7, 0) и
(–7, 0), проходящих через точку (–2, 12).

14.9(764). Написать уравнение линии второго порядка, зная ее фокус
(2, 0), соответствующую ему директрису x = 8 и эксцентриситет е = . Найти второй фокус и вторую директрису линии.

14.10(765). Написать уравнение линии второго порядка, фокус которой находится в точке (2, 0), соответствующая ему директриса имеет уравнение
х = 5, зная, что линия проходит через точку (10, 6). Найти второй фокус и вторую директрису этой линии.

14.11(766). Написать уравнение линии второго порядка, фокус которой находится в точке (2, 0), соответствующая ему директриса имеет уравнение
х = 6, зная, что линия проходит через точку (–4, 8).

14.12(771). Определить эксцентриситет эллипса, если расстояние между фокусами есть среднее арифметическое длин осей.

14.13(772). Найти эксцентриситет эллипса, зная что стороны вписанного в него квадрата проходят через фокусы эллипса.

14.14(778). Дана парабола . Написать уравнение другой параболы, имеющей с данной параболой общую фокальную хорду, т. е. хорду, проходящую через фокус параболы и перпендикулярную к ее оси.

14.15(781). Написать уравнение гиперболы, зная четыре точки (±4, ±2) пересечения ее директрис и асимптот.

14.16(785*). Написать уравнение равносторонней гиперболы, зная ее фокус (1, 1) и асимптоту х + у = 0.

14.17(787*). Составить уравнение эллипса, фокусы которого имеют координаты (1, 0), (0, 1) и большая ось равна 2.

14.18(791). Найти геометрическое место центров окружностей, касающихся данной окружности и не пересекающей ее прямой.

14.19(797). Составить уравнение гиперболы в полярных координатах, если дано ее каноническое уравнение .

Таблица 14.1. Сравнительный анализ характеристик кривых второго порядка

	Парабола	Эллипс	Гипербола
1. Определение
2. Каноническое уравнение		,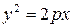
3. Фокусы		,
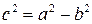
4. Фокальный параметр
5. Эксцентриситет
,	,
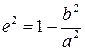6. Расстояние от фокуса до директрисы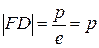
7. Расстояние от начала координат до директрисы
8. Основной прямоугольник	–	,