 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Решения избранных задач 1 страница
|
|
В данном разделе предлагаются решения следующих задач: 1.9, 5.6, 7.1, 7.2, 7.3, 7.4, 7.6(1), 12.14, 12.15.
Задача 1.9
Из точки О выходят два вектора,  =
=  ,
,  =
=  . Найти какой-нибудь вектор
. Найти какой-нибудь вектор  =
= 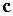 , идущий по биссектрисе угла АОВ.
, идущий по биссектрисе угла АОВ.
Решение
Для решения этой задачи достаточно использовать правило параллелограмма, вспомнив при этом, что диагональ в параллелограмме является биссектрисой, если параллелограмм является ромбом, то есть все его стороны оказываются равными. Поэтому достаточно от векторов  и
и  перейти к векторам
перейти к векторам  и
и  , которые направлены также как
, которые направлены также как  и
и  , соответственно, но имеют одинаковые длины
, соответственно, но имеют одинаковые длины  . В качестве векторов
. В качестве векторов  и
и  можно взять орты векторов
можно взять орты векторов  и
и  :
:  и
и  . Тогда искомое выражение для вектора
. Тогда искомое выражение для вектора 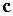 будет выглядеть следующим образом:
будет выглядеть следующим образом:
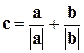 .
.
Можно предложить и другие решения этой задачи, например:
 ,
,  и т.д. и т.п.
и т.д. и т.п.
Задача 5.6
Представить вектор  в виде суммы двух векторов, один из которых параллелен заданному ненулевому вектору
в виде суммы двух векторов, один из которых параллелен заданному ненулевому вектору  , а другой перпендикулярен.
, а другой перпендикулярен.
Решение
1) В задаче требуется представить вектор  в следующем виде
в следующем виде
 ,
,
где  – параллелен вектору
– параллелен вектору  , а
, а  – перпендикулярен
– перпендикулярен  .
.
2) Для  в силу его параллельности ненулевом вектору
в силу его параллельности ненулевом вектору  следует существование такого числа
следует существование такого числа 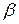 , что
, что  . Тогда вектор
. Тогда вектор  оказывается равным
оказывается равным
 .
.
3) Вектор  перпендикулярен
перпендикулярен  , следовательно, их скалярное произведение равно нулю:
, следовательно, их скалярное произведение равно нулю:
 .
.
Из этого уравнения уже можно найти величину 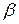 :
:
 .
.
4) Теперь можно выписать искомое выражение для вектора  :
:
 .
.
Для перпендикулярной составляющей пока (до следующего раздела) получаем следующее выражение:
 .
.
5) Во время решения задачи мы получили общую формулу для проекции одного вектора на другой, ведь  ни что иное, как проекция вектора
ни что иное, как проекция вектора  на вектор
на вектор  . Таким образом
. Таким образом
 .
.
Задача 7.1
Представить заданный данный вектор  в виде разложения произвольного вектора по трем заданным некомпланарным векторам
в виде разложения произвольного вектора по трем заданным некомпланарным векторам  ,
,  и
и 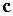 .
.
Решение
По условию задачи необходимо представить вектор  в следующем виде:
в следующем виде:
 . (7.1.1)
. (7.1.1)
Искомые коэффициенты  ,
, 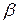 и
и  представляют собой не что иное, как координаты вектора
представляют собой не что иное, как координаты вектора  в базисе, составленном из векторов
в базисе, составленном из векторов  ,
,  и
и  . Существование и единственность такого представления исследована в [2] (см. теоремы 7, 8 в разделах 3, 4).
. Существование и единственность такого представления исследована в [2] (см. теоремы 7, 8 в разделах 3, 4).
Для решения задачи воспользуемся тем свойством смешанного произведения, согласно которому смешанное произведение, содержащее два одинаковых вектора, равно нулю. Умножим скалярно левую и правую часть соотношения (7.1.1) на векторное произведение  :
:
 . (7.1.2)
. (7.1.2)
Отсюда можно найти коэффициент 
 . (7.1.3)
. (7.1.3)
Заметим, что согласно условию задачи величина  , стоящая в знаменателе не равна нулю. Полученный результат можно переписать другим образом:
, стоящая в знаменателе не равна нулю. Полученный результат можно переписать другим образом:
 . (7.1.4)
. (7.1.4)
Аналогично получаем коэффициенты  и
и 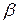 умножая соотношение (7.1.1) на величины
умножая соотношение (7.1.1) на величины  и
и 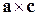 , соответственно:
, соответственно:

 . (7.1.5)
. (7.1.5)
Коэффициент в разложении вектора по базису равен дроби, в знаменателе которой стоит смешанное произведение базисных векторов, а в числителе – это же смешанное произведение, в котором данный вектор стоит вместо базисного вектора, соответствующего искомой координате.
Задача 7.2
Упростить выражение
 .
.
Решение
Для решения задачи рассмотрим двойное векторное произведение  , где в качестве первого вектора возьмем
, где в качестве первого вектора возьмем  , второго –
, второго –  , а третьего –
, а третьего –  . Тогда
. Тогда
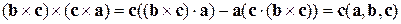 .
.
Умножая это произведение на  получаем
получаем
 .
.
Таким образом, мы показали, что некомпланарность векторов  ,
,  и
и  эквивалентна некопланарности векторов
эквивалентна некопланарности векторов  ,
,  и
и  , то есть величины
, то есть величины
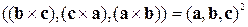
равны (или не равны) нулю одновременно.
Задача 7.3
Определить вектор  по заданным скалярным произведениям
по заданным скалярным произведениям  ,
, 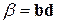 и
и  .
.
Решение
Предложим такое разложение вектора  , чтобы после соответствующих скалярных умножений получалось наиболее простые выражения, желательно содержащие по одному из неизвестных коэффициентов разложения. Одно и таких разложений имеет вид:
, чтобы после соответствующих скалярных умножений получалось наиболее простые выражения, желательно содержащие по одному из неизвестных коэффициентов разложения. Одно и таких разложений имеет вид:
 . (7.3.1)
. (7.3.1)
Действительно, после скалярного умножения на любой из векторов  ,
,  и
и  справа будет оставаться только одно из слагаемых. В тоже время слева будут получаться заданные по условию задачи соответствующие скалярные произведения. Например:
справа будет оставаться только одно из слагаемых. В тоже время слева будут получаться заданные по условию задачи соответствующие скалярные произведения. Например:
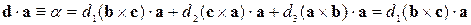 . (7.3.2)
. (7.3.2)
Отсюда получаем:
 . (7.3.3)
. (7.3.3)
Аналогично и для других коэффициентов:
 и
и  . (7.3.4)
. (7.3.4)
В итоге, для вектора  получаем окончательное выражение
получаем окончательное выражение
 . (7.3.5)
. (7.3.5)
Мы видим, что для существования решения необходимо по крайней мере чтобы знаменатели в (7.3.5) не равнялись нулю, то есть векторы  ,
,  и
и  не были компланарными.
не были компланарными.
Задача 7.4 (продолжение задачи 5.6)
Найти компонент вектора  ортогональный вектору
ортогональный вектору  .
.
Решение
В задаче 5.6 был найден компонент  вектора
вектора  параллельный ненулевому вектору
параллельный ненулевому вектору  :
:
 .
.
Отсюда можно найти компонент  вектора
вектора  перпендикулярный вектору
перпендикулярный вектору  :
:
 .
.
Теперь приведем правую часть этого выражения к общему знаменателю:
 .
.
В числителе стоит не что иное, как двойное векторное произведение  . Значит, искомое выражение для
. Значит, искомое выражение для  выглядит так:
выглядит так:
 .
.
Задача 7.6(1)
Доказать, что
 .
.
Решение
Величина  представляет собой смешанное произведение трех векторов
представляет собой смешанное произведение трех векторов  . Следовательно, в нем можно переставить знаки местами:
. Следовательно, в нем можно переставить знаки местами:
 .
.
В фигурных скобках стоит двойное векторное произведение, которое раскрываем согласно правилу:

Раскрывая фигурные скобки, окончательно получаем искомое соотношение.
 .
.
Отметим частный случай соотношения  , в котором векторы
, в котором векторы  и
и  , а также
, а также  и
и  совпадают:
совпадают:
 .
.
Это соотношения связывает длины векторного и скалярного произведения двух векторов:
 .
.
Причем последнее соотношение может быть доказано прямо из определений длин векторного и скалярного произведения:
 .
.
Это равенство справедливо в силу соотношения  .
.
Задача 12.14
Определить проекцию точки на прямую в пространстве, расстояние от этой точки  до прямой
до прямой  . Получить уравнение перпендикуляра, опущенного из этой точки на прямую.
. Получить уравнение перпендикуляра, опущенного из этой точки на прямую.
Решение
1. Пусть точка  является проекцией заданной точки
является проекцией заданной точки  на прямую
на прямую  , причем
, причем  . Тогда вектор
. Тогда вектор  является компонентом вектора
является компонентом вектора  перпендикулярным
перпендикулярным  :
:
 , (12.14.1)
, (12.14.1)
где  – любая точка заданной прямой.
– любая точка заданной прямой.
Так как точка  принадлежит прямой, то ее радиус-вектор может быть записан в виде
принадлежит прямой, то ее радиус-вектор может быть записан в виде  , где
, где  – значение параметра, соответствующее точке
– значение параметра, соответствующее точке  . Тогда для
. Тогда для  получаем:
получаем:
 . (12.14.2)
. (12.14.2)
Длина этого вектора определяет расстояние  от точки
от точки  до прямой:
до прямой:
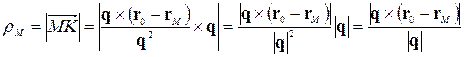 . (12.14.3)
. (12.14.3)
2. Можно найти расстояние от точки до прямой чисто геометрическим методом. Давайте соединим точку  с любой точкой на прямой, например с точкой
с любой точкой на прямой, например с точкой  . Выберем на прямой другую точку, не совпадающую с
. Выберем на прямой другую точку, не совпадающую с  , например
, например  (
( ), и отложим от точки
), и отложим от точки  отрезок
отрезок  , параллельный отрезку
, параллельный отрезку  , так, чтобы точки
, так, чтобы точки  и
и  оказались в одной полуплоскости.
оказались в одной полуплоскости.
Площадь полученного параллелограмма будет равна величине векторного произведения  , в высота, проведенная из точки
, в высота, проведенная из точки  к основанию
к основанию  является искомым расстоянием от точки
является искомым расстоянием от точки  до прямой. Высоту параллелограмма можно найти, разделив его площадь на длину основания, к которому проведена эта высота:
до прямой. Высоту параллелограмма можно найти, разделив его площадь на длину основания, к которому проведена эта высота:
 . (12.14.4)
. (12.14.4)
В это равенство подставим выражения для радиус-векторов точек  и
и  , принадлежащих прямой:
, принадлежащих прямой:

 . (12.14.5)
. (12.14.5)
Особенностью такого решения является то, что в качестве точек  и
и  можно выбирать какие угодно несовпадающие точки прямой. Например, можно было выбрать такие точки
можно выбирать какие угодно несовпадающие точки прямой. Например, можно было выбрать такие точки  и
и  , чтобы
, чтобы 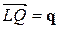 , и сразу получить искомый результат, совпадающий с (12.14.3).
, и сразу получить искомый результат, совпадающий с (12.14.3).
3. Однако полное решение этой задачи требует, чтобы мы нашли еще и местоположение точки  – проекции точки
– проекции точки  на заданную прямую. Эту задачу решим чуть по-другому.
на заданную прямую. Эту задачу решим чуть по-другому.
Пусть точка  на прямой задана своим параметром:
на прямой задана своим параметром:
 . (12.14.6)
. (12.14.6)
Чтобы найти значение  , потребуем, чтобы вектор
, потребуем, чтобы вектор  был ортогонален прямой, то есть
был ортогонален прямой, то есть 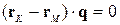 . Тогда имеем
. Тогда имеем
 . (12.14.7)
. (12.14.7)
Отсюда получаем, что
 . (12.14.8)
. (12.14.8)
Следовательно, радиус-вектор точки  равен
равен
 . (12.14.9)
. (12.14.9)
Зная  , можно задать уравнение перпендикуляра, например, как уравнение прямой, проходящей через две точки.
, можно задать уравнение перпендикуляра, например, как уравнение прямой, проходящей через две точки.
Кроме того, можно проверить согласованность разных решений. Так для разности  мы теперь получаем выражение
мы теперь получаем выражение
 , (12.14.10)
, (12.14.10)
из которого следует (12.14.3).


Рис. 12.1. Расстояние от точки до прямой и между скрещивающимися прямыми
Задача 12.15
Найти расстояние между скрещивающимися прямыми. Построить уравнение общей нормали.
Решение
Эту задачу тоже можно решать в три этапа. Сначала найдем расстояние между скрещивающимися прямыми. Потом дадим геометрическое объяснение полученного ответа, а затем получим уравнение прямой – общей нормали к данным прямым.
1. Пусть обе прямые заданы векторными параметрическими уравнениями
 и
и  , (12.15.1)
, (12.15.1)
где заданы радиус-векторы точек  и
и  , через которые проходят прямые, их направляющие векторы
, через которые проходят прямые, их направляющие векторы 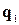 и
и  . Величины
. Величины  и
и  являются параметрами для первой и второй прямой соответственно.
являются параметрами для первой и второй прямой соответственно.
В этом случае сразу можно указать вектор  , перпендикулярный обеим прямым:
, перпендикулярный обеим прямым:
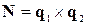 . (12.15.2)
. (12.15.2)
Этот вектор является направляющим вектором для общего перпендикуляра.
Теперь соединим направленным отрезком любую точку на второй прямой  с любой точкой на первой прямой
с любой точкой на первой прямой  :
:
 . (12.15.3)
. (12.15.3)
Предположим, что вектор  , соединяющий точку
, соединяющий точку  на второй прямой с точкой
на второй прямой с точкой  на первой, перпендикулярен обеим прямым. Тогда этот вектор параллелен вектору
на первой, перпендикулярен обеим прямым. Тогда этот вектор параллелен вектору 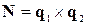 , а длина его равна искомому расстоянию между прямыми
, а длина его равна искомому расстоянию между прямыми  . В то же время точка
. В то же время точка  является ортогональной проекцией точки
является ортогональной проекцией точки  на прямую
на прямую  , а точка
, а точка  – ортогональной проекцией точки
– ортогональной проекцией точки  на прямую
на прямую  . Следовательно, отрезок
. Следовательно, отрезок  есть не что иное, как ортогональная проекция отрезка
есть не что иное, как ортогональная проекция отрезка  на отрезок
на отрезок  или на вектор
или на вектор 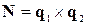 :
:
Дата публикования: 2015-11-01; Прочитано: 3305 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
