Задачи к теме 16

Во всех задачах этой темы система координат – прямоугольная.

16.1(805). С помощью переноса осей координат установить, какая линия определяется каждым из следующих уравнений, и найти ее расположение относительно данной системы координат:

1) 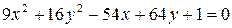;	2) ;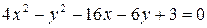
3) 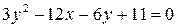;	4) ;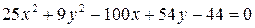
5) 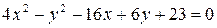;	6) ;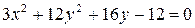
7) 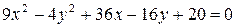;	8) ;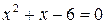
9) 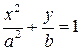;	10) ;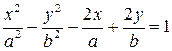
11) .

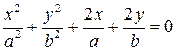16.2(806*). Линия второго порядка определяется уравнением

.

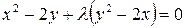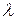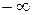Определить тип линии при изменении параметра от до 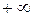и найти ее расположение относительно данной системы координат.

Справочный материал

Теорема про полуинвариант кривой второго порядка. Функция коэффициентов общего уравнения кривой второго порядка

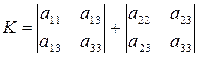
является инвариантом относительно поворотов, а для линий, у которых 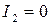и 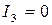, функция инвариантна и при параллельных переносах.

Таблица 16.1. Классификация кривых второго порядка

N			Тип		Название кривой	Уравнение
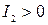
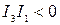
1.	Центральные I2 ≠ 0		Эллиптический		Эллипс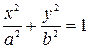
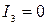
2.		Точка (пара мнимых пересекающихся прямых)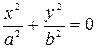
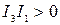
3.		Мнимый эллипс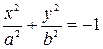
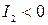
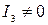
4.		Гиперболический		Гипербола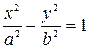
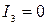
5.		Пара пересекающихся прямых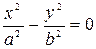
6.	Нецентральные		Параболический		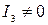Парабола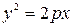
7.	I3=0	K<0	Пара параллельных прямых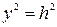
8.	K=0	Пара совпадающих прямых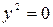
9.	K>0	Пара параллельных мнимых прямых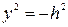

Алгоритм определения вида кривой второго порядка с помощью инвариантов