Введение понятия комплексного числа. Представление комплексного числа на плоскости

Комплексные числа являются расширением множества действительных чисел. В результате расширения множества действительных чисел было введено понятие мнимой единицы , которая существует на множестве комплексных чисел, но не существует на множестве действительных. Мнимая единица удовлетворяет равенству:

.

(1)

В литературе часто мнимую единицу обозначают через . Тогда комплексное число можно представить в виде:

,

(2)

где носит название действительной части или реальной части и обозначается , а носит название мнимой части и обозначается как . Графически все множество действительных чисел можно представить на бесконечной числовой прямой, при этом комплексные числа можно трактовать как расширение числовой прямой до комплексной плоскости, а каждое комплексное число можно представить как точку на комплексной плоскости (смотри рисунок 1). При этом все множество действительных чисел будет представляться прямой на комплексной плоскости.

Рисунок 1: Представление комплексного числа на плоскости

Комплексная плоскость делится прямыми реальной части (прямой действительных чисел) и прямой мнимых чисел на четыре четверти. Любое комплексное число ,будет представляться точкой на комплексной плоскости с координатам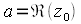и и . Если число не содержит мнимой части, то оно действительное и находится на прямой , а если число не содержит реальной части, то оно называется чисто мнимым и находится на оси .

Такое расширение должно «наследовать» все свойства вещественных чисел, т.е. в этом множестве операции должны подчиняться аксиомам коммутативности, ассоциативности и дистрибутивности:

1. ;

2. ;

3. ;

4. ;

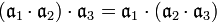5. ;

6.существует нейтральный элемент относительно сложения: ;

7.существует нейтральный элемент относительно умножения: .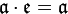

Все указанные равенства должны выполняться для произвольных чисел .

производится отождествление комплексного числа с вещественным числом . Результатом этого является следующая нормальная форма записи комплексного числа

Для числа получаем одно определяющее равенство:

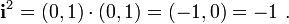
Из соображений упрощения записи, договорились число записывать просто в виде , а числа и записывать в виде и .

Польза от нормальной формы записи состоит в том, что она упрощает действия с комплексными числами. В самом деле, перемножение двух комплексных чисел, представленных в нормальной форме,можно начать производить по обычным правилам перемножения вещественных чисел:

а затем воспользоваться равенством :

Мы получили тот же результат, что формально определен аксиомой.

Если — целое число, то число

называется -й степенью числа .

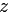Для вычисления при и 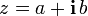можно применить формулу бинома Ньютона:

Определение 1. Алгебраическое расширение поля действительных чисел с помощью элемента , являющегося корнем многочлена , называется полем комплексных чисел ¹⁾. Поле комплексных чисел обозначается через .

Предложение 1. Каждое ассоциативное коммутативное кольцо с единицей и без делителей нуля, являющееся двумерным векторным пространством над полем , изоморфно полю .

Теорема 1.(Основная теорема алгебры.) Поле комплексных чисел алгебраически замкнуто.

Определение 2. Полем комплексных чисел называется множество всех упорядоченных пар действительных чисел . При этом каждая такая пара называется комплексным числом ²⁾. Таким образом, множество комплексных чисел можно интерпретировать как точки на плоскости . Определим операцию сложения комплексных чисел по правилу

для всех ,

и определим операцию умножения:

для всех .

4. Комплексные числа на плоскости. Модуль и аргумент числа, тригонометрическая форма. Сопряженные числа и их свойства.

Комплексным числом называется выражение вида a + ib, где a и b – любые действительные числа, i – некоторый символ, который называется мнимой единицей. Часто используют символическую запись .

Комплексные числа часто обозначают одной буквой, например, z = a + ib. Действительное число a называется действительной частью комплексного числа z, действительная часть обозначается a = Re z. Действительное число b называется мнимой частью комплексного числа z, мнимая часть обозначается b = Im z.

Геометрической интерпретацией действительных чисел является координатная прямая. Кроме того, как было установлено выше, на координатной прямой «нет места для новых точек», то есть любой точке на координатной оси отвечает действительное число. Следовательно, комплексные числа на этой прямой расположить уже нельзя, однако можно попытаться рассмотреть наряду с действительной осью, на которой мы будем откладывать действительную часть комплексного числа, ещё одну ось, ей перпендикулярную, и назвать её мнимой осью. Тогда любому комплексному числу z = x + iy можно поставить в соответствие точку координатной плоскости. На оси абсцисс будем откладывать действительную часть комплексного числа, а на оси ординат будем откладывать мнимую часть комплексного числа. Таким образом, мы построим взаимнооднозначное соответствие между всеми комплексными числами и всеми точками плоскости. Если такое соответствие построено, то координатная плоскость называется комплексной плоскостью.

Важной является интерпретация комплексного числа z = a + ib как вектора OA с координатами (a, b) на комплексной плоскости с началом в точке (0, 0) и концом в точке с координатами (a, b). Это соответствие является взаимнооднозначным.

Модулем комплексного числа называется длина вектора, соответствующего этому числу. Модуль комплексного числа z обычно обозначается | z | или r. Аргументом комплексного числа z = a + ib (z ≠ 0) называется величина угла между положительным направлением действительной оси и вектором z; величина угла считается положительной, если отсчёт производится против часовой стрелки, и отрицательным в противном случае. Угол φ, аргумент комплексного числа, обозначается φ = arg z. Для числа z = 0 аргумент не определён.

Пусть и φ = arg z. Тогда можно записать:

z = a + bi = r (cos φ + i sin φ).

Такая форма записи комплексного числа называется тригонометрической формой записи комплексного числа. Для того, чтобы перейти от алгебраической формы записи комплексного числа к тригонометрической форме, нужно найти его модуль и один из аргументов.

Также используется показательная форма записи комплексного числа:

При этом считается, что .