Связь между матрицами и линейными преобразованиями

Пусть -- некоторый базис в -мерном пространстве и -- линейное преобразование в .

Для любых векторов существует одно и только одно линейное преобразование , такое что

Докажем это. Покажем сначала, что преобразование однозначно определяется векторами . Действительно, пусть

(1)

-- произвольный вектор из . Тогда

и, следовательно, однозначно определяется по .

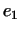Теперь покажем, что для всяких векторов существует линейное преобразование , такое, что . Для этого поставим в соответствие векторам векторы ; произвольному же вектору поставим в соответствие вектор . Так как вектор выражается через однозначно, то ему ставится в соответствие вполне определенный вектор . Легко проверить, что так определенное преобразование линейно.

Обозначим координаты вектора в базисе через , т.е. положим

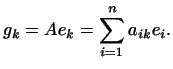
(3)

Совокупность чисел () образует матрицу

которую мы назовем матрицей линейного преобразования в базисе .

Итак, мы доказали, что при заданном базисе каждому линейному преобразованию однозначно соответствует матрица , и, обратно, каждой матрице однозначно отвечает линейное преобразование, определяемое формулами (3), (1), (2).

Мы видим, таким образом, что линейные преобразования можно описывать с помощью матриц и матрицы являются тем аналитическим аппаратом, с помощью которого изучаются линейные преобразования в конечномерных пространствах.

Заметим, что при изменении базиса матрица, соответствующая данному линейному преобразованию, вообще говоря, изменится.