Көрсеткішті үлестірім. Анықтамасы және сандық сипаттамалары

Ықтималдық тығыздығы

мұндағы параметр, теңдiгiмен анықталатын Х кездейсоқ шамасын көрсеткiштiк заң бойынша үлестiрiмдi деп атайды. Анықтама. Егер Х кездейсоқ шамасы мына үлестірім тығыздығы

арқылы берілсе, онда ол көрсеткіштік үлестірім заңымен берілген дейді. Мұндағы - тұрақты оң шама.

Интегралдық функциясын табайық:

.

Сонымен

Бұл үлестірімнің сандық сипаттамалары:

= яғни .

яғни

Кездейсоқ шаманың (а; b) аралығынан мән қабылдау ықтималдығы

;

18. Нормальды үлестірілген кездейсоқ шама. Оның сандық сипаттамаларын қорытып шығар. Мысал келтір.

Нормальді үлестірімдердің композициясы нормальді үлестірілген болады. Осылай егер Х пен У – тәуелсіз нормальді үлестірілген кездейсоқ шамалар болса, яғни, болса онда кездейсоқ шамасы да нормаль үлестірілген болады Х пен У тәуелді болса, (корреляция коэффициенті ρ≠0), онда Z=X+Y нормальді үлестірілген болып қалады, параметрлері

болады.

Үздіксіз кездейсоқ Х шамасының ықтималдықтар үлестірімін қалыпты деп атайды, егер оның ықтималдықтар үлестірім заңы ықтималдық тығыздығымен анықталса

. (1)

мұндағы нақты параметрлер Бұл кездейсоқ шаманың математикалық үмітін табайық:

,

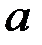яғни .Сонымен параметр қалыпты заң үшін математикалық үміт болады.Енді дисперсиясын табайық:

Өйткені мүшелеп интегралдасақ

болады. Сонымен, , ал 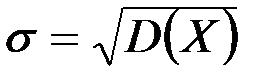орташа квадраттық ауытқуы болады.Қалыпты үлестірімі бар кездейсоқ шаманың математикалық үміті мен дисперсиясын есептеп отырып, оның анықтамасына қатынасатын параметрлердің ықтималдық мәнін аштық: бұл анықтамадағы параметрі математикалық үмітті, ал параметрі дисперсияны көрсетеді.

Теорема. Қалыпты үлестірімді кездейсоқ шаманың берілген аралығына түсу ықтималдығы .формуласы бойынша анықталады, мұндағы Лаплас функциясы

19. Көп өлшемді кездейсоқ шама. Көп өлшемді үлестірім функциясы. Маргиналды үлестірімдер. Қасиеттері