 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Закон взаимосвязи массы и энергии
|
|
Важным результатом теории относительности Эйнштейна является универсальное соотношение между энергией т ела и его массой
 . (20)
. (20)
Уравнение (20) выражает фундаментальный закон природы - закон взаимосвязи массы и энергии. В силу однородности времени в релятивистской механике, как и в классической, выполняется закон сохранения энергии:
"полная энергия замкнутой системы сохраняется".
Разложив (20) в ряд и пренебрегая членами второго порядка малости, получим
 (21)
(21)
Величина  (22)
(22)
называется энергией покоя.
В общем случае кинетическая энергия
 .
.
Из формул (20) и (18) следует, что
 , т.е.
, т.е.
 . (23)
. (23)
Анализируя уравнение (20), отметим, что оно имеет универсальный характер, применимо ко всем формам энергии и можно утверждать, что с энергией связана масса
т = Е/с2 (24)
и, наоборот, со всякой массой связано определенное количество энергии (20). Закон взаимосвязи массы и энергии подтверждается при протекании ядерных реакций.
16) Молекулярно-кинетическая теория (сокращённо МКТ) — теория, возникшая в XIX веке и рассматривающая строение вещества, в основном газов, с точки зрения трёх основных приближенно верных положений:
· все тела состоят из частиц: атомов, молекул и ионов;
· частицы находятся в непрерывном хаотическом движении (тепловом);
· частицы взаимодействуют друг с другом путём абсолютно упругих столкновений.
МКТ стала одной из самых успешных физических теорий и была подтверждена целым рядом опытных фактов. Основными доказательствами положений МКТ стали: Диффузия, Броуновское движение, Изменение агрегатных состояний вещества
 Основное уравнение МКТ связывает макроскопические параметры (давление, объём, температура) термодинамической системы с микроскопическими (масса молекул, средняя скорость их движения).
Основное уравнение МКТ связывает макроскопические параметры (давление, объём, температура) термодинамической системы с микроскопическими (масса молекул, средняя скорость их движения).
Е=3/2kT, т.е Т=2Е/3k или p=nkT где Т=р/nk
17) Молекулы можно рассматривать как системы материальных точек (атомов) совершающих как поступательное, так и вращательное движения. При исследовании движения тела необходимо знать его положение относительно выбранной системы координат. Для этого вводится понятие о степенях свободы тела. Число независимых координат, которые полностью определяют положение тела в пространстве, называется числом степеней свободы тела.
При движении точки по прямой линии для оценки ее положения необходимо знать одну координату, т.е. точка имеет одну степень свободы. Если точка движения по плоскости, ее положение характеризуется двумя координатами; при этом точка обладает двумя степенями свободы. Положение точки в пространстве определяется 3 координатами. Число степеней свободы обычно обозначают буквой i. Молекулы, которые состоят из обычного атома, считаются материальными точками и имеют три степени свободы (аргон, гелий).
Двухатомные жесткие молекулы, например молекулы водорода, азота и др., обладают пятью степенями свободы: они имеют 3 степени свободы поступательного движения и 2 степени свободы вращения вокруг осей ОХ и OZ. Вращением вокруг оси OY можно пренебречь, т.к. момент инерции ее относительно этой оси пренебрежимо мал. Поэтому вклад энергии вращательного движения вокруг оси OY в суммарную энергию двухатомной молекулы можно не учитывать.
Молекулы, состоящие из трех и более жестко связанных атомов, не лежащих на одной прямой, имеют число степеней свободы i = 6: три степени свободы поступательного движения и 3 степени свободы вращения вокруг осей ОХ, OY и OZ.
В этом случае, если расстояние между атомами может изменяться (нежесткие молекулы), появляются дополнительные степени свободы.
Согласно молекулярно-кинетической теории газов движение молекул носит беспорядочный характер; эта беспорядочность относится ко всем видам движения молекулы. Ни один из видов движения не имеет преимущества перед другим. При статистическом равновесии движений энергия в среднем распределяется равномерно между всеми видами движения. Закон равномерного распределения энергии по степеням свободы молекул можно сформулировать следующим образом: статистически в среднем на каждую степень свободы молекул приходится одинаковая энергия. Поступательное движение молекул характеризуется средней кинетической энергией, равной 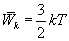 . Так как поступательному движению соответствует 3 степени свободы, то в среднем на одну степень свободы движения молекул приходится энергия
. Так как поступательному движению соответствует 3 степени свободы, то в среднем на одну степень свободы движения молекул приходится энергия

В однородном газе, молекулы которого имеют любое число степеней свободы i, каждая молекула в среднем обладает энергией движения, равной

|
Средняя энергия может быть вычислена так 
 внутренняя энергия.
внутренняя энергия.
Итак, средняя энергия приходящаяся на одну степень свободы:

| (4.4.1) |
У одноатомной молекулы i = 3, тогда для одноатомных молекул

| (4.4.2) |
для двухатомных молекул

| (4.4.3) |
для трёхатомных молекул

| (4.4.4) |
Таким образом, на среднюю кинетическую энергию молекулы, имеющей i-степеней свободы, приходится

| (4.4.5) |
Это и есть закон Больцмана о равномерном распределении средней кинетической энергии по степеням свободы.
18) Закон Максвелла для распределения молекул по скоростям и энергиям. В газе, находящемся в состоянии равновесия, устанавливается стационарное распределение молекул по скоростям, подчиняющееся определенному статистическому закону. Этот закон был выведен теоретически Дж. Максвеллом. Максвелл предполагал, что вещество состоит из очень большого числа тождественных молекул, находящихся в состоянии беспорядочного теплового движения при одинаковой температуре. Также предполагалось, что силовые поля на газ не действуют.
Закон Максвелла описывается некоторой функцией f(v), называемой функцией распределения молекул по модулям скоростей. Если разбить диапазон скоростей молекул на малые интервалы, равные dv, то на каждый интервал скорости будет приходиться некоторое число молекул dN(v), скорости которых заключены в этом интервале.
Функция f(v) определяет относительное число молекул dN(v)/N, скорости которых лежат в интервале от v до v+dv, то есть:
dN(v)/N=f(v)dv, откуда f(v)=dN(v)/Ndv (28)
Применяя методы теории вероятностей, Дж. Максвелл нашел вид функции распределения молекул идеального газа по модулям скоростей хаотического движения:
 (29)
(29)
Из (29) следует, что конкретное распределение зависит от рода газа (от массы молекулы) и от его термодинамической температуры. Очевидно, что функция распределения не зависит ни от давления, ни от объема газа. График функции распределения имеет вид, показанный на рис. 5.

Рис. 5. График функции распределения молекул по скоростям
Выражение dN(v)/N=f(v)dv представляет собой вероятность встретить молекулу со скоростью, принадлежащей интервалу (v;v+dv). Эта вероятность равна площади заштрихованной полоски с основанием dv (рис. 5). Относительная доля молекул, имеющих определенную скорость, равна нулю.
Площадь под кривой f(v) равна вероятности достоверного события – встретить молекулу со скоростью, принадлежащей интервалу (0;∞), то есть равна единице. Это означает, что функция удовлетворяет условию нормировки:  f(v)dv=1 (30)
f(v)dv=1 (30)
Наиболее вероятная vв, средняя арифметическая <v> и среднеквадратичная скорости <vкв> молекул.
Наиболее вероятная скорость соответствует максимуму функции распределения, ведь именно этой скоростью будет обладать наибольшее число молекул. Ее значение найдется из условия экстремума функции f(v):

vв=√(2kT/m0)=√(2kNAT/m0NA)=√(2RT/M) (31)
Отсюда видно, что при увеличении температуры T максимум кривой распределения сместится вправо, так как при увеличении T увеличивается vв, которая определяет положение максимума. Но площадь под кривой должна оставаться постоянной. Поэтому величина максимума будет уменьшаться. Влияние же массы молекулы m0 будет обратным. Влияние температуры и массы молекулы на вид функции распределения показано на рис. 6.

Рис. 6. Влияние параметров газа на вид функции распределения
Выражение для средней скорости <v> определяется по формуле:
<v>=  vf(v)dv=√(8kT/πm0)=√(8kNAT/πm0NA)=√(8RT/πM) (32)
vf(v)dv=√(8kT/πm0)=√(8kNAT/πm0NA)=√(8RT/πM) (32)
Аналогично найдем выражение для среднеквадратичной скорости: <vкв>=  v2f(v)dv.
v2f(v)dv.
Произведя интегрирование, получим: <vкв>=√(3RT/M) (33)
Из сравнения найденных скоростей вытекает: <vкв>=√(3RT/M) > <v>=√(8RT/πM) > vв=√(2RT/M).
Соотношения между скоростями: vв: <v>: <vкв> = √2: √(8/π): √3 = 1: 1,13: 1,22
Исходя из распределения молекул по скоростям 
можно найти распределение молекул газа по значениям кинетической энергии . Для этого перейдем от переменной v к переменной =m0v2/2. Подставив в (44.4) v=  и dv=
и dv=  d, получим
d, получим
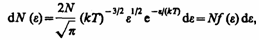
где dN() — число молекул, имеющих кинетическую энергию поступательного движения, заключенную в интервале от до + d.
Таким образом, функция распределения молекул по энергиям теплового движения

Средняя кинетическая энергия <> молекулы идеального газа

19) Барометрическая формула — зависимость давления или плотности газа от высоты в поле силы тяжести.
Для идеального газа, имеющего постоянную температуру  и находящегося в однородном поле тяжести (во всех точках его объёма ускорение свободного падения
и находящегося в однородном поле тяжести (во всех точках его объёма ускорение свободного падения  одинаково), барометрическая формула имеет следующий вид:
одинаково), барометрическая формула имеет следующий вид:

где  — давление газа в слое, расположенном на высоте
— давление газа в слое, расположенном на высоте  ,
,  — давление на нулевом уровне (
— давление на нулевом уровне ( ),
),  — молярная масса газа,
— молярная масса газа,  — универсальная газовая постоянная,
— универсальная газовая постоянная,  — абсолютная температура. Из барометрической формулы следует, что концентрация молекул
— абсолютная температура. Из барометрической формулы следует, что концентрация молекул 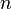 (или плотность газа) убывает с высотой по тому же закону:
(или плотность газа) убывает с высотой по тому же закону:

где  — масса молекулы газа,
— масса молекулы газа,  — постоянная Больцмана.
— постоянная Больцмана.
Барометрическая формула может быть получена из закона распределения молекул идеального газа по скоростям и координатам в потенциальном силовом поле (см. Статистика Максвелла — Больцмана). При этом должны выполняться два условия: постоянство температуры газа и однородность силового поля. Аналогичные условия могут выполняться и для мельчайших твёрдых частичек, взвешенных в жидкости или газе. Основываясь на этом, французский физик Ж. Перрен в 1908 году применил барометрическую формулу к распределению по высоте частичек эмульсии, что позволило ему непосредственно определить значение постоянной Больцмана.
Барометрическая формула показывает, что плотность газа уменьшается с высотой по экспоненциальному закону. Величина  , определяющая быстроту спада плотности, представляет собой отношение потенциальной энергии частиц к их средней кинетической энергии, пропорциональной
, определяющая быстроту спада плотности, представляет собой отношение потенциальной энергии частиц к их средней кинетической энергии, пропорциональной  . Чем выше температура
. Чем выше температура  , тем медленнее убывает плотность с высотой. С другой стороны, возрастание силы тяжести
, тем медленнее убывает плотность с высотой. С другой стороны, возрастание силы тяжести  (при неизменной температуре) приводит к значительно большему уплотнению нижних слоев и увеличению перепада (градиента) плотности. Действующая на частицы сила тяжести
(при неизменной температуре) приводит к значительно большему уплотнению нижних слоев и увеличению перепада (градиента) плотности. Действующая на частицы сила тяжести  может изменяться за счёт двух величин: ускорения
может изменяться за счёт двух величин: ускорения  и массы частиц
и массы частиц  .
.
Следовательно, в смеси газов, находящейся в поле тяжести, молекулы различной массы по-разному распределяются по высоте.
закон больцмана для распределения частиц во внешнем потенциальном поле. Пусть идеальный газ находится в поле консервативных сил в условиях теплового равновесия. При этом концентрация газа будет различной в точках с различной потенциальной энергией, что необходимо для соблюдения условий механического равновесия. Так, число молекул в единичном объеме n убывает с удалением от поверхности Земли, и давление, в силу соотношения P = nkT, падает.
Если известно число молекул в единичном объеме, то известно и давление, и наоборот. Давление и плотность пропорциональны друг другу, поскольку температура в нашем случае постоянна. Давление с уменьшением высоты должно возрастать, потому что нижнему слою приходится выдерживать вес всех расположенных сверху атомов.
Исходя из основного уравнения молекулярно-кинетической теории: P = nkT, заменим P и P0 в барометрической формуле (2.4.1) на n и n0 и получим распределение Больцмана для молярной массы газа:

| (2.5.1) |
где n0 и n - число молекул в единичном объёме на высоте h = 0 и h.
Так как  а
а  , то (2.5.1) можно представить в виде
, то (2.5.1) можно представить в виде

| (2.5.2) |
С уменьшением температуры число молекул на высотах, отличных от нуля, убывает. При T = 0 тепловое движение прекращается, все молекулы расположились бы на земной поверхности. При высоких температурах, наоборот, молекулы оказываются распределёнными по высоте почти равномерно, а плотность молекул медленно убывает с высотой. Так как mgh – это потенциальная энергия U, то на разных высотах U = mgh – различна. Следовательно, (2.5.2) характеризует распределение частиц по значениям потенциальной энергии:
 , ,
| (2.5.3) |
– это закон распределения частиц по потенциальным энергиям – распределение Больцмана. Здесь n0 – число молекул в единице объёма там, где U = 0.
20) Внутренняя энергия – энергия покоя. Она складывается из теплового хаотического движения молекул, составляющих тело, потенциальной энергии их взаимного расположения, кинетической и потенциальной энергии электронов в атомах, нуклонов в ядрах и так далее.
В термодинамических процессах изменяется только кинетическая энергия движущихся молекул (тепловой энергии недостаточно, чтобы изменить строение атома, а тем более ядра). Следовательно, фактически под внутренней энергией в термодинамике подразумевают энергию теплового хаотического движения молекул.
Внутренняя энергия массы m одноатомного идеального газа равна

|
Таким образом, внутренняя энергия зависит только от температуры. Внутренняя энергия U является функцией состояния системы. Понятно, что в общем случае термодинамическая система может обладать как внутренней, так и механической энергией, и разные системы могут обмениваться этими видами энергии.
Обмен механической энергией характеризуется совершенной работой А, а обмен внутренней энергией – количеством переданного тепла Q.
Количество теплоты, сообщаемой телу, идёт на увеличение внутренней энергии и на совершение телом работы:
 , ,
| (4.1.1) |
– это и есть первое начало термодинамики, или закон сохранения энергии в термодинамике.
Правило знаков:  если тепло передаётся от окружающей среды данной системе,
если тепло передаётся от окружающей среды данной системе,  и
и 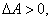 если система производит работу над окружающими телами, при этом
если система производит работу над окружающими телами, при этом  . Учитывая правило знаков, первое начало термодинамики можно записать в виде:
. Учитывая правило знаков, первое начало термодинамики можно записать в виде:
 , ,
|
– изменение внутренней энергии тела равно разности сообщаемой телу теплоты и произведённой телом работы.
Количество энергии, переданное системой (системе) в процессе механического воздействия, называется работой. Работу A принято считать положительной, если она совершается системой (энергия передается от системы внешним телам). Если работа совершается над системой, то работа считается отрицательной. Работу можно вычислить, зная изменение параметров самой системы. Так, например, при изобарном расширении газа работа силы 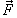 при перемещении поршня на
при перемещении поршня на  равна
равна  . Поскольку F = РS, где P – давление газа, S – площадь поршня, то
. Поскольку F = РS, где P – давление газа, S – площадь поршня, то  . Так как
. Так как  – изменение объема газа, то работа изобарного расширения газа равна
– изменение объема газа, то работа изобарного расширения газа равна
 . .
|
21) Первое начало термодинамики — один из трёх основных законов термодинамики, представляет собой закон сохранения энергии для термодинамических систем. Количество теплоты, полученное системой, идёт на изменение её внутренней энергии и совершение работы против внешних сил.
Тепло  , полученное системой, идет на изменение ее внутренней энергии
, полученное системой, идет на изменение ее внутренней энергии  и совершение работы над внешними телами
и совершение работы над внешними телами 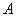 :
:
 .
.
Дата публикования: 2015-11-01; Прочитано: 2130 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
