 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Закон Ома и Джоуля Ленца в интегральной и дифференциальной форме
|
|
Закон Ома в интегральной форме для однородного участка цепи (не содержащего ЭДС)

| (7.6.1) |
Для однородного линейного проводника выразим R через ρ:
 , ,
|
Закон Ома также применяется ко всей цепи, но в несколько изменённой форме:
I=E/(R+r),
где:
e — ЭДС цепи,
I — сила тока в цепи,
R — сопротивление всех элементов цепи,
r — внутреннее сопротивление источника питания.
Исходя из закона Ома (7.6.1), имеем:

А мы знаем, что  или
или 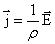 . Отсюда можно записать
. Отсюда можно записать
 , ,
| (7.6.3) |
это запись закона Ома в дифференциальной форме.
Здесь  – удельная электропроводность.
– удельная электропроводность.
Размерность σ – [  ].
].
В случае, когда проводник неподвижен и химических превращений в нем не совершается, работа тока затрачивается на увеличение внутренней энергии проводника, в результате чего проводник нагревается. Принято говорить, что при протекании тока в проводнике выделяется тепло
 (4.1)
(4.1)
Это соотношение называется законом Джоуля - Ленца. Оно было экспериментально установлено английским физиком Д. П. Джоулем и подтверждено точными опытами Э. Х. Ленца.
Если сила тока изменяется со временем, то количество теплоты, выделяющееся в проводнике за время t, вычисляется по формуле
 .
.
От формулы (4.1), можно перейти к выражению, характеризующему выделение тепла в различных точках проводника. Выделим в проводнике элементарный объем в виде цилиндра. Согласно закону Джоуля - Ленца, за время d t, в этом объеме выделится количество теплоты
 ,
,
где - d V элементарный объем. Разделив это выражение на d V и d t, найдем количество теплоты, выделяющееся в единице объема в единицу времени:
 .
.
Величину  называют удельной тепловой мощностью тока. Эта формула представляет собой дифференциальную форму закона Джоуля - Ленца.
называют удельной тепловой мощностью тока. Эта формула представляет собой дифференциальную форму закона Джоуля - Ленца.
39) Сторонние силы - силы неэлектрической природы, вызывающие перемещение электрических зарядов внутри источника постоянного тока. Сторонними считаются все силы отличные от кулоновских сил.
Электродвижущая сила (ЭДС) — физическая величина, характеризующая работу сторонних (непотенциальных) сил в источниках постоянного или переменного тока. В замкнутом проводящем контуре ЭДС равна работе этих сил по перемещению единичного положительного заряда вдоль контура.
ЭДС можно выразить через напряжённость электрического поля сторонних сил
I. Сторонние силы.
Сторонняя электродвижущая сила совершает положительную работу по перемещению положительного заряда в сторону возрастания потенциала, т.е. против сил электростатического поля (вследствие сопротивления потенциал электростатического поля понижается, положительный заряд двигается от большего потенциала к меньшему => должны существовать участки, на которых “+” заряд движется от меньшего потенциала к большему).
Сторонняя сила не может иметь электростатического происхождения т.к. электростатическое поле — потенциальное и А по замкнутому пути =0 и ток не мог бы существовать, т.к. он должен совершать работу для преодоления сопротивления проводника.
Физическая природа сторонних сил весьма различна:
Они могут быть обусловлены:
а) химической, физической неоднородностью проводника при соприкосновении разнородных проводников (гальванические элементы; аккумуляторы—возникает контактная разность потенциалов при контакте твёрдого тела и жидкости)
б) физическая неоднородность при соприкосновении проводников различной температуры (термоэлементы)
в) механические происхождения
г) электрическое происхождение — сила действует на заряд в электростатическом поле, возникающем по закону электромагнитной индукции.
| Обобщенный закон Ома для произвольного участка цепи | Электричество [ Физика ] | |||
|  
| |||
| Произведение силы тока на сопротивление участка цепи равно алгебраической сумме падения потенциала на этом участке и ЭДС всех источников электрической энергии, включенных на данным участке цепи. | ||||
| Обозначение | Описание | |||
| I |
| |||
| R |
| |||
| φ 1 |
| |||
| φ 2 |
| |||
| ξ |
| |||
Дата публикования: 2015-11-01; Прочитано: 5386 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
