 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Уравнение релятивистской динамики
|
|
В ньютоновой механике обычная трехмерная 3-сила определяется как скорость изменения во времени количества движения, переносимого на данное тело от окружающих тел и полей (равенство  Ньютона является одновременно и определением силы, и законом движения). Аналогично поступим и в релятивистской механике, не забывая в то же время, что делить (множить) следует только на инвариантные величины.
Ньютона является одновременно и определением силы, и законом движения). Аналогично поступим и в релятивистской механике, не забывая в то же время, что делить (множить) следует только на инвариантные величины.
По определению 4-сила  - это скорость изменения 4-импульса, оцененная в течение собственного времени движущегося тела (точки; частицы), т.е.
- это скорость изменения 4-импульса, оцененная в течение собственного времени движущегося тела (точки; частицы), т.е.  . Подставляя значение 4-импульса, можно представить 4-силу в виде
. Подставляя значение 4-импульса, можно представить 4-силу в виде

или
 =
=

Подставив значение  и учтя явный вид компонент импульса
и учтя явный вид компонент импульса 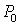 и
и  , получим величину
, получим величину 

| (8.4) |
Так выглядит 4-сила в системе I (в которой время t, скорость  ). Ниже структура
). Ниже структура  будет представлена в более компактном виде.
будет представлена в более компактном виде.
Здесь возникает важный вопрос: если при скоростях значительно меньших скорости света ( ), т.е. в ньютоновой механике, сила определяется по второму закону Ньютона равенством
), т.е. в ньютоновой механике, сила определяется по второму закону Ньютона равенством  (индекс "н" указывает на ньютонову механику), то как следует обобщить понятие 3-силы на любые скорости, вплоть до как угодно близких к скорости света?
(индекс "н" указывает на ньютонову механику), то как следует обобщить понятие 3-силы на любые скорости, вплоть до как угодно близких к скорости света?
Ответ на такие вопросы может давать только практика, эксперименты, опыт. Вся современная экспериментальная физика подтверждает, что под релятивистской 3-силой следует понимать величину, являющуюся производной от релятивистского 3 импульс
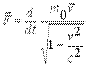
| (8.5) |
Это равенство обобщает ньютонову трактовку 3-силы. В то же время оно представляет основной закон движения частицы (материальной точки) в инерциальной системе отсчета при любых возможных скоростях меньших с.
Рассмотрим закон преобразования компонент 4-силы, представленных формулой (8.4). Учитывая (8.5), представим 4-силу в окончательном виде

| (8.6) |
Как видим, в структуру 4-силы Минковского  входит релятивистская
входит релятивистская
трехмерная сила 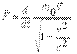 и ее мощность
и ее мощность  .
.
Рассмотрим дальше преобразование компонент 4-силы при переходе от ИСО I к ИСО П, которая движется со скоростью v относительно системы I в направлении оси х. При этом в системе I предполагается известным мгновенное значение скорости точки  (vx,vy,vz) и сила
(vx,vy,vz) и сила  . Преобразование 4-силы позволит определить также и величину трехмерной силы в системе II. Как уже указывалось, преобразование компонент 3-векторов определяется на основе сначала преобразования 4-векторов (при переходе
. Преобразование 4-силы позволит определить также и величину трехмерной силы в системе II. Как уже указывалось, преобразование компонент 3-векторов определяется на основе сначала преобразования 4-векторов (при переходе  ). Итак, нужно подвергнуть компоненты 4-силы
). Итак, нужно подвергнуть компоненты 4-силы 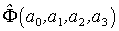 , т.е.
, т.е.
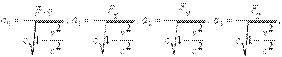
| (8.7) |
преобразованиям Лоренца. Применяя их к (8.7), получим четыре формулы, дающие окончательный вариант преобразований

| (8.8a) |

| (8.8b) |
Следовательно, при переходе от системы отсчет I к системе II проекции 3-силы  изменяются; они остаются неизменными в нерелятивистском случае, когда
изменяются; они остаются неизменными в нерелятивистском случае, когда 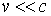 . Первая из полученных формул определяет мощность силы в системе II, остальные три - проекции силы.
. Первая из полученных формул определяет мощность силы в системе II, остальные три - проекции силы.
15) Релятивистское выражение для энергии
В релятивистской механике справедливым остается выражение
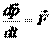 .
.
Это означает, что 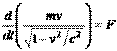 . Откуда видно, что сила не является инвариантной величиной. Кроме того, сила F и ускорение a не коллениарны.
. Откуда видно, что сила не является инвариантной величиной. Кроме того, сила F и ускорение a не коллениарны.
Легко получить выражение для кинетической энергии. Поскольку
dEk = dA и dEk = v · p · dt, dA = F · ds
 .
.
Отсюда следует, что E0 = mc2 является энергией покоя. Энергия и импульс в релятивистской механике не сохраняются. Инвариантом является выражение:

Взаимосвязь массы и энергии. Границы применимости механики Ньютона.
Дата публикования: 2015-11-01; Прочитано: 1518 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
