Работа переменной силы

Рассмотрим материальную точку, движущуюся под действием силы Р по прямой. Если действующая сила постоянна и направлена вдоль прямой, а перемещение равно s, то, как известно из физики, работа А этой силы равна произведению Ps. Теперь выведем формулу для подсчета работы, совершаемой переменной силой.

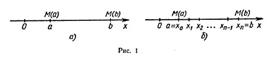
Пусть точка движется по оси Ох под действием силы, проекция которой на ось Ох есть функция f от х. При этом мы будем предполагать, что f есть непрерывная функция. Под действием этой силы материальная точка переместилась из точки М (а) в точку М (b) (рис. 1, а). Покажем, что в этом случае работа А подсчитывается по формуле

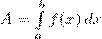(1)

Разобьем отрезок [а; b] на п отрезков одинаковой длины .Это отрезки [а; x₁], [x₁; x₂],..., [x_n-1;b] (рис. 1,6). Работа силы на всем отрезке [а; b] равна сумме работ этой силы на полученных отрезках. Так как f есть непрерывная функция от x, при достаточно малом отрезке [а; x₁] работа силы на этом отрезке приблизительно равна f (а) (x₁—а) (мы пренебрегаем тем, что f на отрезке меняется). Аналогично работа силы на втором отрезке [x₁; x₂] приближенно равна f (x₁) (x₂ — x₁) и т. д.; работа силы на n-ом отрезке приближенно равна f (x_n-1)(b — x_n-1). Следовательно, работа силы на всем отрезке [а; b] приближенно равна:

и точность приближенного равенства тем выше, чем короче отрезки, на которые разбит отрезок [а;b] Естественно, что это приближенное равенство переходит в точное, если считать, что n→∞:

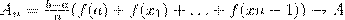
Поскольку A_n при n →∞ стремится к интегралу рассматриваемой функции от а до b, формула (1) выведена.

Кинетическая энергия

Чтобы сообщить телу ускорение и заставить его двигаться с определенной скоростью, нужно совершить работу. Эта работа запасается в виде кинетической энергии тела.

Если:
W_к — Кинетическая энергия тела, энергия движения (Джоуль),
m — масса тела (кг),
s — перемещение тела (метр)
u — скорость тела (м/c)
a — ускорение тела (м/c²)

Кинетическая энергия тела, энергия движения, записывается в виде формулы:

1.	Wк = mas = mu 2

Изменение величины скорости от u₁ до u₂ приводит к изменению кинетической энергии, которое записывается в виде:

2.	ΔWк = m (u 22− u 12)

Если u₂ < u₁, то выражение в скобках отрицательно, ΔW_к<0, т.е. тело отдает свою кинетическую энергию.

10) Все силы, встречающиеся в механике, принято разделять на консервативные и неконсервативные.

Сила, действующая на материальную точку, называется консервативной (потенциальной), если работа этой силы зависит только от начального и конечного положений точки. Работа консервативной силы не зависит ни от вида траектории, ни от закона движения материальной точки по траектории (см. рис. 2): .

Изменение направления движения точки вдоль малого участка на противоположное вызывает изменение знака элементарной работы 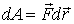, следовательно, . Поэтому работа консервативной силы вдоль замкнутой траектории 1 a 2 b 1 равна нулю: .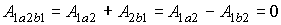

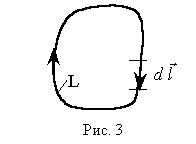Точки 1и 2, а также участки замкнутой траектории 1 a 2 и 2 b 1 можно выбирать совершенно произвольно. Таким образом, работа консервативной силы по произвольной замкнутой траектории L точки ее приложения равна нулю:

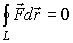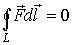или . (5)

В этой формуле кружок на знаке интеграла показывает, что интегрирование производится по замкнутой траектории. Часто замкнутую траекторию L называют замкнутым контуром L (рис. 3). Обычно задаются направлением обхода контура L по ходу часовой стрелки. Направление элементарного вектора перемещения совпадает с направлением обхода контура L. В этом случае формула (5) утверждает: циркуляция вектора по замкнутому контуру L равна нулю.

Следует отметить, что силы тяготения и упругости являются консервативными, а силы трения неконсервативными. В самом деле, поскольку сила трения направлена в сторону, противоположную перемещению или скорости, то работа сил трения по замкнутому пути всегда отрицательна и, следовательно, не равна нулю.

Потенциальное поле сил- Если тело поставлено в такие условия, что в каждой точке пространства оно подвержено воздействию других тел с силой закономерно изменяющейся от точки к точке говорят, что это тело находится в поле сил. Так, например, тело вблизи поверхности Земли находится в поле сил тяжести — в - каждой точке пространства на него действует сила P=mg направленная по вертикали вниз.

В качестве второго примера, рассмотрим тело M, «привязанное» пружиной к некоторому центру.O(Рис, 56). Один конец пружины может вращаться на шарнире вокруг неподвижной точки O в любом направлении, другой конец

Рис. 56.

прикреплен к телу M.В каждой точке пространства на тело M действует сила, направленная по радиусу (т. е, вдоль прямой, проходящей через центр O и тело M) и равная

(26.1)

где r — расстояние тела от центра O, r₀— длина недеформированной пружины, k — коэффициент пропорциональности. Если r>r₀ (пружина растянута), сила направлена к центру и имеет знак «—» (направления силы и радиуса - вектора противоположны); если r<r₀ (пружина сжата), сила - направлена от центра, и имеет знак «+» Рассмотренное поле сил представляет собой частный случай так называемого поля центральных сил, характерного тем, что направление силы, действующей в любой точке пространства, проходит через некоторый центр, а величина силы зависит только от расстояния до этого центра f=f(r)

Поле сил тяжести тоже является частным случаем центрального поля сил.

Приведенные примеры характерны тем, что силы, действующие на тело, зависят только от положения тела в пространстве (точнее, от положения тела по отношению к другим действующим на него телам) и не зависят от скорости тела.

Для сил, зависящих только от положения тела, может случиться, что работа, совершаемая ими над телом не зависит от пути, а определяется только начальным и конечным положениями тела в пространстве. В этом случае поле сил называется потенциальным, а сами силы — консервативными. Силы, работа которых зависит от пути, по которому тело переходит из одного положения в другое, называются неконсервативными.

Работа консервативных сил на любом замкнутом пути равна нулю. В самом деле, разобьем замкнутый путь» по которому совершает обход тело, находящееся в потенциальном поле, на две части: путь 1, по которому тело переходит из точки 1 в точку 2, и путь //, по которому тело переходит из точки 2 в точку 1 причем точки 1 и 2 выберем совершенно произвольно (рис, 57).

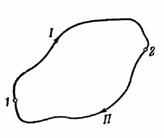
Рис. 57.

Рис. 58.

Работа на всем замкнутом пути будет равна сумме работ, совершаемых на каждом из участков:

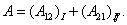
(26.2)

Покажем, что работа, совершаемая на каком-либо пути, например на пути 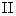(рис. 57), при переходе тела по нему из точки 1 в точку 2 равна взятой с обратным знаком работе, совершаемой на том же пути при обратном переходе из точки 2 в точку 1. Рассмотрим участок траектории Δs (рис. 58). Поскольку в потенциальном поле сила f зависит только от положения тела в пространстве и не зависит от состояния движения тела (в частности, от направления движения), элементарная работа на пути Δs при движении в одном направлении равна ΔA=fΔs, при движении же в другом направлении она равна 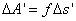. Так как 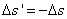, то . Это справедливо для любого элементарного участка пути, а, следовательно, и для работы на всем пути, так что

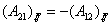
(26.3)

Воспользовавшись полученным результатом, равенство (26.2) можно записать следующим образом:

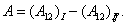
(26.4)

Но в потенциальном поле сил работа не зависят от пути, т. е. (A₁₂)₁=(A₁₂)₁₁. Следовательно, выражение (26.4) равно пулю, что и требовалось доказать.

Если работа каких-то сил на любом замкнутом пути равна нулю, то работа этих сил при переходе тела из одного положения в другое; очевидно, не зависит от пути (это можно доказать, обратив ход проведенных выше рассуждений). Поэтому потенциальное поле сил можно определить как поле таких сил, работа которых на любом замкнутом пути равна нулю. Поскольку работа в потенциальном поле сил на замкнутом пути равна нулю, на одних участках замкнутого пути силы совершают положительную работу, а на других — отрицательную. Работа сил трения за промежуток времени Δt согласно (24.10) равна

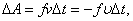
так как векторы fuv все время имеют противоположные направления[1]. Следовательно, работа сил трения все время остается отрицательной и на замкнутом пути будет отлична от нуля. Таким образом, силы трения принадлежат к числу неконсервативных сил.

Докажем, что поле сил тяжести является потенциальным. Сила, действующая на тело в любой точке траектории, имеет одинаковую величину P=mg и направление - вниз по вертикали (рис. 59). Поэтому согласно (24.12) работа равна:

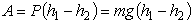(26.5)

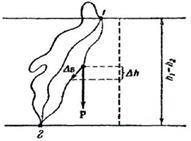
Рис. 59.

Это выражение, очевидно, не зависит от пути, откуда следует, что поле сил тяжести потенциально.

Поле центральных сил также потенциально. Элементарная работа на пути Δs (рис. 60) равна:

ΔA=f(r) Δs_f

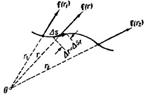
Рис. 60.

Но проекция Δs на направление силы в данном месте, т. е. на направление радиуса-вектора r равна Δr — приращению расстояния тела от точки О: Δs_f=Δr. Поэтому

ΔA=f(r)Δr

Работа на всем пути

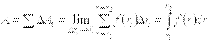
Последнее выражение зависит, очевидно, только от вида функции f(r) и от значений r₁ иr₂. От ряда траектории оно никак не зависит, поэтому центральное поле сил тоже потенциально.