Релятивистский импульс

Уравнения классической механики инвариантны по отношению к преобразованиям Галилея, по отношению же к преобразованиям Лоренца они оказываются неинвариантными. Из теории относительности следует, что уравнение динамики, инвариантное по отношению к преобразованиям Лоренца, имеет вид:

где - инвариантная, т.е. одинаковая во всех системах отсчета величина называемая массой покоя частицы, v- скорость частицы, 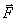- сила действующая на частицу. Сопоставим с классическим уравнением

Мы приходим к выводу, что релятивистский импульс частицы равен

(6.7)

Релятивистская масса.

Определив массу частицы m как коэффициент пропорциональности между скоростью и импульсом, получим, что масса частицы зависит от ее скорости.

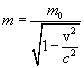
(6.8)

Энергия в релятивистской динамике.

Для энергии частицы в теории относительности получается выражение:

(6.9)

Из (2.3) следует, что покоящаяся частица обладает энергией

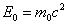
(6.10)

Эта величина носит название энергии покоя частицы. Kинетическая энергия, очевидно, равна

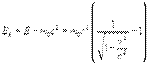
(6.11)

Приняв во внимание, что , выражение для полной энергии частицы можно написать в виде

(6.12)

Из последнего выражения вытекает, что энергия и масса тела всегда пропорциональны друг другу. Всякое изменение энергии тела сопровождается изменением массы тела

и, наоборот, всякое изменение массы сопровождается изменениемэнергии . Это утверждение носит название закона взаимосвязи или закона пропорциональности массы и энергии.