 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Теорема Гаусса для электрического поля в среде
|
|
 (3)
(3)
т. е. поток вектора смещения электростатического поля в диэлектрике сквозь любую замкнутую поверхность равен алгебраической сумме свободных электрических зарядов, заключенных внутри этой поверхности. В такой форме теорема Гаусса верна для электростатического поля как для однородной и изотропной, так и для неоднородной и анизотропной сред.
Для вакуума Dn = ε0En (ε=1), и поток вектора напряженности Е сквозь произвольно выбранную замкнутую поверхность равен

Так как источниками поля Е в среде являются как свободные, так и связанные заряды, то теорему Гаусса для поля Е в самом общем виде можно записать как

где ∑Qi и ∑Qsv— соответственно алгебраические суммы свободных и связанных зарядов, которые охватываются замкнутой поверхностью S. Но эта формула неприменима для описания поля Е в диэлектрике, поскольку она выражает свойства неизвестного поля Е через связанные заряды, которые, в свою очередь, определяются им же. Это еще раз показывает целесообразность введения вектора электрического смещения.
Напряженность электростатического поля, как следует из ранее полученной формулы E=E0/ε, зависит от свойств среды: в однородной изотропной среде напряженность поля Е обратно пропорциональна ε. Вектор напряженности Е, при переходе через границу диэлектриков, испытывает скачкообразное изменение, тем самым делая неудобства при расчетах электростатических полей. Поэтому необходимо помимо вектора напряженности характеризовать поле еще вектором электрического смещения, который для электрически изотропной среды, по определению, равен
 (1)
(1)
Поскольку ε=1+θ и P =θε0 E, вектор электрического смещения равен
 (2)
(2)
Единица электрического смещения — кулон на метр в квадрате (Кл/м2).
32) Распределение заряда на проводнике. Если зарядить изолированный проводник, заряд распределится только на поверхности проводника по следующим причинам:
· поскольку одноимённые заряды отталкиваются, избыточные электрические заряды стремятся расположиться как можно дальше друг от друга; это соответствует распределению заряда на поверхности;
· то же можно доказать с помощью теоремы Гаусса: поля внутри проводника быть не может (иначе заряды ещё бы двигались, и не было бы равновесия), следовательно, и поток поля через любую замкнутую поверхность, построенную внутри проводника, равен нулю; из теоремы Гаусса тогда следует, что внутри проводника нет нескомпенсированных электрических зарядов.
Заряд должен распределиться по поверхности проводника таким образом, что бы эта поверхность была эквипотенциальной. Иначе вдоль поверхности существовало бы электрическое поле, что приводило бы к перемещению зарядов, то есть не было бы равновесия.
Электрическое поле, созданное зарядами на изолированном проводнике, всегда направлено перпендикулярно поверхности проводника. Это поле не приводит к движению зарядов, ибо заряды не могут покинуть проводник (на поверхности металла существует потенциальный барьер, "запирающий" электроны внутри металла, так называемая "работа выхода электрона из металла").
В проводниках могут перемещаться свободно не только заряды принесенные из вне, но и микроскопические заряды, из которых состоят атомы и молекулы проводника (электроны, ионы). Поэтому при помещении незаряженного проводника во внешнее электрическое поле 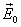 свободные микроскопические заряды будут перемещаться к его поверхности: положительные по полю, а отрицательные против поля. На одном конце проводника будет скапливаться избыток положительного заряда, а на другом избыток отрицательного до тех пор, пока создаваемое этими зарядами дополнительное поле
свободные микроскопические заряды будут перемещаться к его поверхности: положительные по полю, а отрицательные против поля. На одном конце проводника будет скапливаться избыток положительного заряда, а на другом избыток отрицательного до тех пор, пока создаваемое этими зарядами дополнительное поле 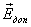 не скомпенсирует внешнее поле во всех точках внутри проводника. При этом суммарное поле
не скомпенсирует внешнее поле во всех точках внутри проводника. При этом суммарное поле  внутри проводника и на его поверхности будет удовлетворять условию
внутри проводника и на его поверхности будет удовлетворять условию  и
и 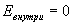 т.е. внутри проводника
т.е. внутри проводника  , а в близи проводника будет заметно отличаться от своего первоначального значения
, а в близи проводника будет заметно отличаться от своего первоначального значения  . Заряды на противоположных краях проводника называются индуктированными или наведенными.
. Заряды на противоположных краях проводника называются индуктированными или наведенными.
Индуктивные заряды распределяются по внешней поверхности проводника. Если внутри проводника имеется полость, то при равновесном распределении индуцированных зарядов поле внутри нее также равно нулю. На этом основана электростатическая защита.
Электростатическая защита — помещение приборов, чувствительных к электрическому полю, внутрь замкнутой проводящей оболочки для экранирования от внешнего электрического поля.
Это явление связано с тем, что на поверхности проводника (заряженного или незаряженного), помещённого во внешнее электрическое поле, заряды перераспределяются так (явление электростатической индукции), что создаваемое ими внутри проводника поле полностью компенсирует внешнее.
33) Конденса́тор (от лат. condensare — «уплотнять», «сгущать») — двухполюсник с определённым или переменным значением ёмкости и малой проводимостью; устройство для накопления заряда и энергии электрического поля.
Конденсатор является пассивным электронным компонентом. В простейшем варианте конструкция состоит из двух электродов в форме пластин (называемых обкладками), разделённых диэлектриком
Емкость конденсатора. Свойство конденсатора накапливать и удерживать электрические заряды характеризуется его емкостью. Чем больше емкость конденсатора, тем больше накопленный им заряд, так же как с увеличением вместимости сосуда или газового баллона увеличивается объем жидкости или газа в нем.
Емкость С конденсатора определяется как отношение заряда q, накопленного в конденсаторе, к разности потенциалов между его электродами (приложенному напряжению)U:
C = q / U (69)
Емкость конденсатора измеряется в фарадах (Ф).
Рассмотрим уединенный проводник, которому сообщается некоторый электрический заряд Q. Как мы знаем, этот электрический заряд распределяется по поверхности проводника и в окружающем пространстве создает электрическое поле. Напряженность этого поля не постоянна, она изменяется как по величине, так и по направлению (рис. 355).

рис. 355
Но потенциал проводника постоянен во всех его точках. Очевидно, что данный потенциал пропорционален заряду проводника. Следовательно, отношение заряда проводника к его потенциалу не зависит от величины электрического заряда, поэтому это отношение является «чистой» характеристикой проводника, находящегося в определенной среде, которая называется электрической емкостью проводника (электроемкостью).
Итак, электроемкостью проводника называется отношения электрического заряда проводника к его потенциалу

Как неоднократно было сказано, электрический потенциал определяется с точностью до произвольной постоянной. Во избежание неопределенности, в определении (1) полагают, что потенциал стремится к нулю при бесконечном удалении от рассматриваемого проводника:

Можно дать эквивалентное определение: электроемкость проводника равна электрическому заряду, который необходимо сообщить проводнику, чтобы повысить его потенциал на единицу1.
34 ) Потенциальную энергию взаимодействия двух точечных зарядов q1 и q2, находящихся в вакууме на расстоянии r12 друг от друга можно вычислить по:
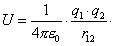 (1)
(1)
Рассмотрим систему, состоящую из N точечных зарядов: q1, q2,..., qn.
Энергия взаимодействия такой системы равна сумме энергий взаимодействия зарядов взятых попарно:
 . (2)
. (2)
В формуле 2 суммирование производится по индексам i и k (i№k). Оба индекса пробегают, независимо друг от друга, значения от 0 до N. Слагаемые, для которых значение индекса i совпадает со значением индекса k не учитываются. Коэффициент 1/2 поставлен потому, что при суммировании потенциальная энергия каждой пары зарядов учитывается дважды. Формулу (2) можно представить в виде:
 , (3)
, (3)
где ji - потенциал в точке нахождения i-го заряда, создаваемый всеми остальными зарядами:
 .
.
Энергия взаимодействия системы точечных зарядов, вычисляемая по формуле (3), может быть как положительной, так и отрицательной. Например она отрицательная для двух точечных зарядов противоположного знака.
Формула (3) определяет не полную электростатическую энергию системы точечных зарядов, а только их взаимную потенциальную энергию. Каждый заряд qi, взятый в отдельности обладает электрической энергией. Она называется собственной энергией заряда и представляет собой энергию взаимного отталкивания бесконечно малых частей, на которые его можно мысленно разбить. Эта энергия не учитывается в формуле (3). Учитывается только работа затрачиваемая на сближение зарядов qi, но не на их образование.
Полная электростатическая энергия системы точечных зарядов учитывает также работу, на образование зарядов qiиз бесконечно малых порций электричества, переносимых из бесконечности. Полная электростатическая энергия системы зарядов всегда положительная. Это легко показать на примере заряженного проводника. Рассматривая заряженный проводник как систему точечных зарядов и учитывая одинаковое значение потенциала в любой точке проводника, из формулы (3) получим:
 . (4)
. (4)
Эта формула дает полную энергию заряженного проводника, которая всегда положительна (при q>0, j>0, следовательно W>0, если q<0, то j<0, но W>0).
35)Энергия заряженного конденсатора и проводника. Если на обкладках конденсатора электроемкостью С находятся электрические заряды +q и - q, то согласно формуле (20.1) напряжение между обкладками конденсатора равно

В процессе разрядки конденсатора напряжение между его обкладками убывает прямо пропорционально заряду q от первоначального значения U до 0.
Среднее значение напряжения в процессе разрядки равно

Для работы А, совершаемой электрическим полем при разрядке конденсатора, будем иметь:

Следовательно, потенциальная энергия Wp конденсатора электроемкостью С, заряженного до напряжения U, равна

Энергия конденсатора обусловлена тем, что электрическое поле между его обкладками обладает энергией. Напряженность Е поля пропорциональна напряжению U, поэтому энергия электрического поля пропорциональна квадрату его напряженности.
36) Энергия и плотность энергии электрического поля. Рассмотрим однородное электрическое поле плоского конденсатора. С одной стороны, энергия заряженного конденсатора 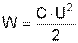 . С другой стороны, эту же энергию можно выразить через напряженность электрического поля Е. Так как
. С другой стороны, эту же энергию можно выразить через напряженность электрического поля Е. Так как
U = E . d и  ,
,
гдеd – расстояние между обкладками конденсатора; S – площадь обкладок, то
 . (1.17)
. (1.17)
Здесь V = Sd – объем электрического поля между обкладками конденсатора.
Формула (1.17) показывает, что энергия заряженного конденсатора (а также любого заряженного проводника) сосредоточена (локализована) в поле, окружающем проводник.
Для характеристики распределения энергии в поле вводится понятие объемной плотности энергии w, Для случая однородного поля:
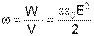 . (1.18)
. (1.18)
 . (1.19)
. (1.19)
где D = ee0E – вектор электрической индукции.
Таким образом, свойства электрического поля характеризуются не только напряженностью Е и потенциалом j, но энергией W и плотностью энергии w. Так как энергия связана с массой соотношением

где с – скорость распространения света в вакууме, то масса m0 единицы объема электрического поля равна
 .
.
Энергия является мерой движения материи, и понятие о материи не может рассматриваться оторвано от понятия энергии. Электрическое поле – один из видов материи.
37)Электрический ток. Сила и плотность тока.
Электри́ческий ток — направленное (упорядоченное) движение заряженных частиц[1][2][3]. Такими частицами могут являться: в металлах — электроны, в электролитах — ионы (катионы и анионы), в газах — ионы и электроны, в вакууме при определенных условиях — электроны, в полупроводниках — электроны и дырки (электронно-дырочная проводимость). Иногда электрическим током называют также ток смещения, возникающий в результате изменения во времени электрического поля[4].
Электрический ток имеет следующие проявления:
· нагревание проводников (в сверхпроводниках не происходит выделения теплоты);
· изменение химического состава проводников (наблюдается преимущественно в электролитах);
· создание магнитного поля (проявляется у всех без исключения проводников)[3]
Различают переменный (англ. alternating current, AC), постоянный (англ. direct current, DC) и пульсирующий электрические токи, а также их всевозможные комбинации.
Постоянный ток — ток, направление и величина которого слабо меняются во времени.
Переменный ток — ток, величина и направление которого меняются во времени.
Пульсирующий ток — ток, у которого изменяется только величина, а направление остаётся постоянным.
Сила тока - скалярная физическая величина, равная отношению заряда, прошедшего через проводник, ко времени, за которое этот заряд прошел.

где I - сила тока, q - величина заряда (количество электричества), t - время прохождения заряда.
Плотность тока - векторная физическая величина, равная отношению силы тока к площади поперечного сечения проводника.

Электрический ток имеет количественные характеристики: скалярную — силу тока, и векторную — плотность тока.
Сила тока — физическая величина, равная отношению количества заряда, прошедшего за некоторое время через поперечное сечение проводника, к величине этого промежутка времени.
Сила тока в Международной системе единиц (СИ) измеряется в амперах (русское обозначение: А).
По закону Ома сила тока 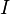 на участке цепи прямо пропорциональна напряжению
на участке цепи прямо пропорциональна напряжению  , приложенному к этому участку цепи, и обратно пропорциональна его сопротивлению
, приложенному к этому участку цепи, и обратно пропорциональна его сопротивлению  :
:
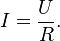
Если на участке цепи электрический ток не постоянный, то напряжение и сила тока постоянно изменяется, при этом у обычного переменного тока среднее значения напряжения и силы тока равны нулю. Однако средняя мощность выделяемого при этом тепла нулю не равна. Поэтому применяют следующие понятия:
· мгновенные напряжение и сила тока, то есть действующие в данный момент времени.
· амплитудные напряжение и сила тока, то есть максимальные абсолютные значения
· эффективные (действующие) напряжение и сила тока определяются тепловым действием тока, то есть имеют те же значения, которые они имеют у постоянного тока с таким же тепловым эффектом.[8]
Плотность тока — вектор, абсолютная величина которого равна отношению силы тока, протекающего через некоторое сечение проводника, перпендикулярное направлению тока, к площади этого сечения, а направление вектора совпадает с направлением движения положительных зарядов, образующих ток.
Согласно закону Ома в дифференциальной форме плотность тока в среде  пропорциональна напряжённости электрического поля
пропорциональна напряжённости электрического поля  и проводимости среды
и проводимости среды  :
:

Для существования постоянного электрического тока необходимо наличие свободных заряженных частиц и наличие источника тока. в котором осуществляется преобразование какого-либо вида энергии в энергию электрического поля.
Дата публикования: 2015-11-01; Прочитано: 5387 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
