Бесконечно малые функции и их свойства

Определение 3. Функция называется бесконечно малой функцией в точке или функцией класса , если При этом пишут Таким образом,

Например, функция а функции не являются функциями класса

Теорема 3. Имеют место следующие свойства класса

Если то т.е.

Доказательство. Свойство очевидно. Докажем свойство (другие свойства доказываются аналогично). Пусть и Тогда для произвольного существуют числа 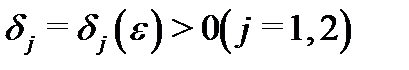такие, что

Выберем 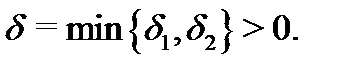Тогда будут иметь место одновременно неравенства (2) и (3). Складывая их, получим, что

Это и означает, что т.е. верно свойство . Теорема доказана.

Следующая теорема устанавливает связь между бесконечно малыми функциями и функциями, имеющими предел при

Теорема 4. Если существует (конечный) предел то Обратно: если функция представляется в виде то имеет предел в точке и

Доказательство. Существование предела эквивалентно высказыванию

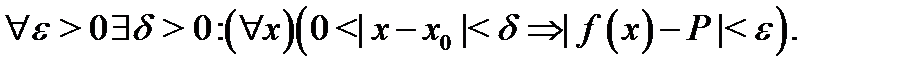
Высказывание (4), в свою очередь, эквивалентно тому, что функция т. е. что Теорема доказана.

Замечание 2. Равенство называют асимптотическим разложением функции имеющей предел в точке

И, наконец, дадим определение предела функции в бесконечности. Сделаем это кратко.

Определение 4. Множества

называются окрестностями точек 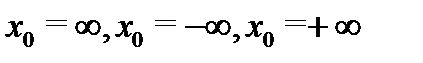соответственно. Следующие высказывания являются определениями предела функции в бесконечности:

Перейдем теперь к обоснованию арифметических действий над пределами.

Теорема 5. Если существуют (конечные) пределы то и существуют пределы при этом

Если (кроме существования пределов и ) выполняется ещё условие то существует предел причем

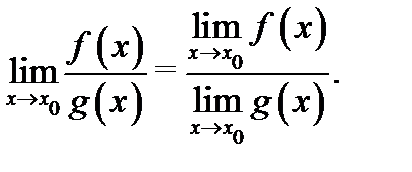
Доказательство. Докажем, например, теорему о пределе произведения. Так как существуют пределы то по теореме 4 имеют место асимптотические разложения Умножая эти равенста друг на друга, будем иметь Поскольку то (см. теорему 3). Далее, поскольку то функция представляется в виде По теореме 14 отсюда следует, что существует предел произведения при и он равен

Теорема доказана.

6. Эквивалентные бесконечно малые. Таблица эквивалентных бесконечно малых

Введем следующее понятие. Пусть конечная или бесконечная точка и пусть функ-

ции и определены в некоторой проколотой окрестности точки

Определение 4. Две бесконечно малые функции и (при ) называются

эквивалентными, если в некоторой проколотой окрестности и если

При этом пишут:

Важность этого понятия становится ясной при формулировке следующего утверждения.

Теорема 6. Если и если существует предел то существует и предел и он также равен числу

Доказательство. Переходя в тождестве к пределу при и учитывая, что получаем утверждение теоремы.

Используя эту теорему, а также таблицу эквивалентных бесконечно малых:

Таблица 1.

Если при то при верны следующие соотношения:

const.

можно без особого труда вычислять пределы конкретных функций.

Пример 1.