 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Задачи о пути, пройденном точкой при неравномерном движении
|
|
Пусть по прямой движется точка с переменной скоростью, для которой известен закон измерения V=v(t) Требуется найти путь S. Пройденный точкой за промежуток времени [0;T]. Если бы скорость была постоянной, то путь легко было бы найти по известной формуле S=VT. В данном случае этой формулой воспользоваться нельзя. Поступим следующим образом.
Разобьем отрезок времени [0;T]. Произвольно на достаточно малые промежутки точками: 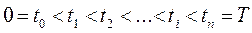
Длительность каждого элементарного промежутка времени равна 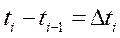 . Если
. Если 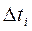 достаточно малы, то с некоторой погрешностью скорость на каждом элементарном отрезке можно считать постоянной. Тогда путь, пройденный точкой за промежуток
достаточно малы, то с некоторой погрешностью скорость на каждом элементарном отрезке можно считать постоянной. Тогда путь, пройденный точкой за промежуток 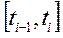 ,
, 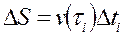 , где
, где 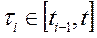 и выбирается произвольно на этом отрезке (i=1, 2, …, n).
и выбирается произвольно на этом отрезке (i=1, 2, …, n).
Весь путь 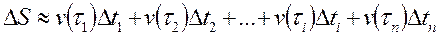 , или
, или 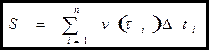
Чем меньше 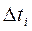 , тем меньше погрешность в каждом слагаемом
, тем меньше погрешность в каждом слагаемом 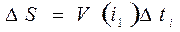 При стремлении
При стремлении 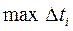 к нулю получаем
к нулю получаем 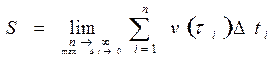 (12.1)
(12.1)
Задача о площади криволинейной трапеции.
|
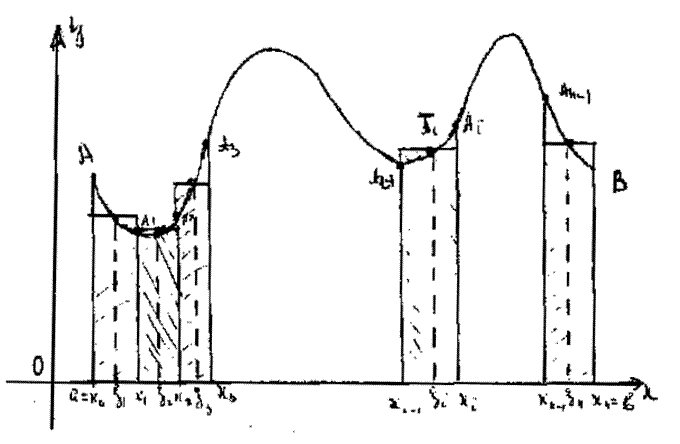 Криволинейной трапецией называется плоская фигура, ограниченная кривой
Криволинейной трапецией называется плоская фигура, ограниченная кривой 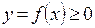 , прямыми x =a, x =b и осью абсцисс y =0.
, прямыми x =a, x =b и осью абсцисс y =0.
На рис.10.1 аАВb - криволинейная трапеция. Требуется найти площадь SаАВb. Разобьем отрезок 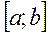 произвольно на n элементарное отрезков точками
произвольно на n элементарное отрезков точками 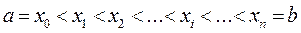 . Длина каждого элементарного отрезка
. Длина каждого элементарного отрезка 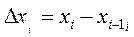 для i =1, 2, …, n. Из точек xi восставим перпендикуляры до пересечения с прямой АВ. На кривой получим точки
для i =1, 2, …, n. Из точек xi восставим перпендикуляры до пересечения с прямой АВ. На кривой получим точки 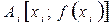 Криволинейная трапеция аАВb разбилась на n элементарных криволинейных трапеций (полосочек) с основаниями
Криволинейная трапеция аАВb разбилась на n элементарных криволинейных трапеций (полосочек) с основаниями  Обозначим площадь элементарной криволинейной трапеции
Обозначим площадь элементарной криволинейной трапеции 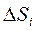 . На отрезке
. На отрезке 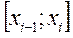 выберем произвольную точку
выберем произвольную точку 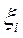 . Если
. Если 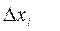 достаточно малы, то с некоторой погрешностью можно площадь элементарной трапеции считать равной площади прямоугольника с основанием
достаточно малы, то с некоторой погрешностью можно площадь элементарной трапеции считать равной площади прямоугольника с основанием 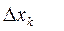 и высотой
и высотой 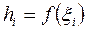 . То есть
. То есть
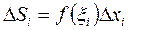
В этом случае площадь криволинейной трапеции с некоторой погрешностью равна площади ступенчатой фигуры, состоящей из элементарных прямоугольников.
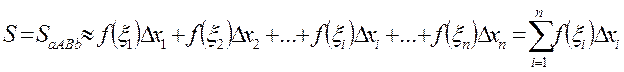
Погрешность тем меньше, чем больше n и чем меньше  .
.
Очевидно
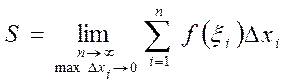 (12.2)
(12.2)
в) задача об объеме продукции, произведенный за некоторый промежуток времени.
Пусть функция y=f(t) Описывает производительность некоторого производства (человека, бригады, механизма, танка) в течение промежутка времени [0;T]. По аналогии с задачей а) разобьем промежуток времени [0;T] точками 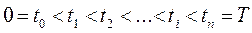 . На достаточно малые промежутки длительностью
. На достаточно малые промежутки длительностью 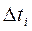 . В этом случае можно полагать, что объем произведенной продукции за этот промежуток
. В этом случае можно полагать, что объем произведенной продукции за этот промежуток 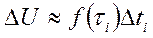 ,где
,где 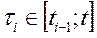 . Погрешность в равенстве тем меньше, чем меньше
. Погрешность в равенстве тем меньше, чем меньше 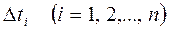 Тогда объем произведенной продукции:
Тогда объем произведенной продукции:
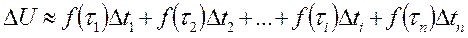
Если 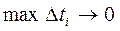 , то
, то
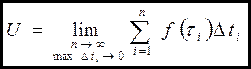 (12.3)
(12.3)
Анализ рассмотренных задач показывает, что различные по смысловому содержанию задачи абсолютно одинаковы по математической схеме. Поэтому есть смысл рассмотреть произвольную функцию y=f(x) на отрезке 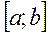 , используя выше приведенную схему.
, используя выше приведенную схему.
1. разобьем отрезок 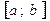 произвольно на n элементарных отрезков точками
произвольно на n элементарных отрезков точками 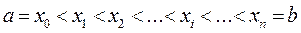 .
.
2. На отрезке 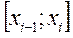 выберем произвольную точку, которой соответствует значение функции
выберем произвольную точку, которой соответствует значение функции  .
.
3.Составим произведения 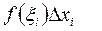 и найдем
и найдем 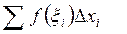 . Назовем эту сумму интегральной суммой для функции f(x) на отрезке
. Назовем эту сумму интегральной суммой для функции f(x) на отрезке 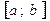 . Очевидно эта интегральная сумма зависит как от способа разбиения
. Очевидно эта интегральная сумма зависит как от способа разбиения 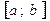 точками
точками  , так и от выбора точек
, так и от выбора точек 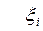 .
.
 Определение. Если существует конечный предел интегральной суммы при
Определение. Если существует конечный предел интегральной суммы при 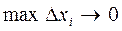 , не зависящий от способа выбор точек
, не зависящий от способа выбор точек 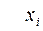 и
и 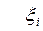 , то он называется определенным интегралом от функции f(x) на отрезке
, то он называется определенным интегралом от функции f(x) на отрезке 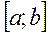 , а функция f(x) называется интегрируемой на этом отрезке.
, а функция f(x) называется интегрируемой на этом отрезке.
При этом вводится обозначение

f(x) - подынтегральная функция, выражение
f(x)dx - подынтегральное выражение
a и b - нижний и верхний предел соответственно.
Возвращаясь к рассмотренным выше задачам можно заметить, что путь, пройденный точкой за промежуток времени [0;T]. С переменной скоростью V=v(t):
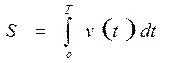 (12.4)
(12.4)
Площадь криволинейной трапеции
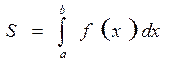 (12.5)
(12.5)
Объем произведенной продукции за промежуток [0;T] при изменяющей производительности Z=z(t)
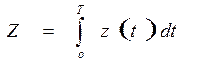 (12.6)
(12.6)
Из (12.5) следует геометрический смысл определенного интеграла: он представляет собой площадь криволинейной трапеции при условии, что 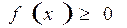 на отрезке
на отрезке 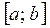 . А из (12.6) вытекает экономический смысл определенного интеграла: если
. А из (12.6) вытекает экономический смысл определенного интеграла: если 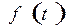 - производительность труда, то определенный интеграл представляет объем произведенной продукции за промежуток времени [0;T].
- производительность труда, то определенный интеграл представляет объем произведенной продукции за промежуток времени [0;T].
Замечание. Следует иметь ввиду, что определенный и неопределенный интегралы существенно различаются. Если 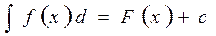 - представляет собой семейство функций (кривых), то определенный интеграл
- представляет собой семейство функций (кривых), то определенный интеграл 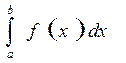 - есть некоторое число.
- есть некоторое число.
Дата публикования: 2015-11-01; Прочитано: 268 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
