 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Свойства неопределенного интеграла
|
|
1.  .
.
Действительно, если  – первообразная для функции
– первообразная для функции  , то
, то
 , что и требовалось доказать.
, что и требовалось доказать.
2.  .
.
3.  .
.
4.  .
.
Докажем это свойство
Найдем

Следовательно

и окончательно
 , что и требовалось доказать..
, что и требовалось доказать..
5  .
.
Доказательство аналогично свойству 4.
6.Инвариантность формулы исследования.
 Формула интегрирования сохраняет вид, если в нее вместо независимой переменной х подставить любую дифференцируемую функцию
Формула интегрирования сохраняет вид, если в нее вместо независимой переменной х подставить любую дифференцируемую функцию  , то есть
, то есть 

Доказательство.
Пусть  и
и 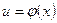 – дифференцируемая функция. Рассмотрим сложную функцию
– дифференцируемая функция. Рассмотрим сложную функцию 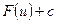 .
.

Примеры.
 ,
,  ,
, 
Таблица основных интегралов.
1.  7.
7. 
2.  8.
8. 
3.  9.
9. 
4.  10.
10. 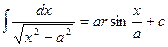
5.  11.
11. 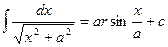
6.  12.
12. 
Замечание. Не путать интегралы 9 с 11 и 10 с 12.
Задача успешного интегрирования состоит в умении свети интеграл к табличному.
Примеры.






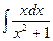
Некоторые методы интегрирования.
Дата публикования: 2015-11-01; Прочитано: 200 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
