Метод подстановки

Метод подстановки (или метод замены переменной) – один из основных методов интегрирования. Рассмотрим , где – непрерывная и дифференцируемая функция. Тогда

(11.1)

Докажем.

Отсюда

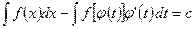
Так как неопределенные интегралы определены с точностью до постоянной, то отбросив указанную постоянную, получим формулу (11.1).

Смысл использования замены - от заданного интеграла перейти к более простому или даже табличному.

Пример 1.

Замечание. Часто удобно вводить замену 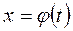в неявном виде, то есть рассматривать новую переменную t как функцию от х .

Пример 2.

.

Пример 3

.

Интегрирование некоторых выражений, содержащих в знаменателе квадратный трехчлен.

1.

В случае обоих знаков получим табличные интегралы.

2.

Для первого интеграла введем замену тогда .

В результате .

Окончательно

3. Пример.

Для первого интеграла введем замену .

Тогда