 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Экстремум функции двух переменных
|
|
Понятия экстремума (максимума и минимума) для функции двух (и нескольких) переменных вводятся так же, как и для функции одной переменной.
Определение. Точка М0 (x0 , y0) называется точкой максимума (минимума) функции z = f(x,y)=, f(M), если существует окрестность этой точки, такая, что для всех точек М (x, y) из этой окрестности выполняется неравенство 
( (рис. 10.7 и 10.8)
Рис.10.7
Рис. 10.8
Как и функция одной переменной, функция двух переменных может в рассматриваемой области иметь несколько максимумов и минимумов, которые не следует путать с наибольшими (наименьшими) значениями функции в этой области.
Теорема. (Необходимое условие существование экстремума). Если точка М0 (x0 , y0) есть точка экстремума дифференцируемой функции z = f(x,y), то ее частные производные в этой точке 
и 
.
Доказательство. Пусть точка М0 (x0 , y0) – точка максимума. В этом случае функция одной переменной f(x,y0) имеет максимум, значит, 
. Аналогично 
.
Пример. Рассмотрим функцию z = x*y, ее частные производные 
и 
обращаются в ноль в точке О(0,0). Но очевидно, что значения функции в этой точке z = 0. Однако легко показать, что в окрестности этой точки функция может принимать значения и больше и меньше нуля, то есть экстремума в ней нет.
Значит, равенство нулю частных производных первого порядка в некоторой точке не является достаточным для существования экстремума функции в этой точке. Точки, в которых частные производные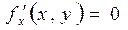 
и 
(или не существуют) называются критическими точками этой функции. Очевидно, точки экстремума следует искать среди критических точек.
Теорема. (Достаточное условие существования экстремума функции двух переменных). Пусть функция 
:
а) определена в некоторой окрестности критической точки М0 (x0 , y0);
б) имеет в этой точке непрерывные частные производные второго порядка 
, 
, 
. Тогда если 
, в точке М0 (x0 , y0) функция имеет экстремум; причем, если А>0 (C>0) – минимум, если А<0(C<0) – то максимум. При 
< 0 функция в точке М0 (x0 , y0) не имеет экстремума. Если 
, вопрос о наличии экстремума остается открытым.
Пример. Найти экстремум функции 
Найдем критические точки.
 |
М0 (-4, 1) – критическая точка. Исследуем эту точку на экстремум.
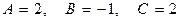
Функция имеет в точке М0 (-4, 1) экстремум. Так как А=2>0, то в точке М0 данная точка имеет минимум, и минимальное значение функции 
Дата публикования: 2015-11-01; Прочитано: 260 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
