 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Функции от одномерной случайной величины
|
|
Пусть случайная величина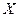 
задана на вероятностном пространстве 
. Случайная величина 
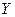, которая каждому элементарному исходу 
ставит в соответствие число 
, называется функцией 
от случайной величины .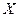
Функция от дискретной случайной величины – дискретная случайная величина, так как она не может принимать больше значений, чем случайная величина .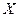
V А меньше?
| 
| 
| … | 
|
| 
| 
| … | 
|
|
| 
| 
| … | 
|
|
|
| 
| … | 
|
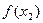
Если 
, то 
.
V
| 
| 
| 
| 
| 
|
| 
| 
|
| 
|
|
| 
| 
| 
| 
| 
|
|
|
|
|
|
|
|
|
| 
|
|
|
| 
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 
| 
| 
| 
|
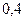
Функция 
от непрерывной случайной величины может быть как непрерывной, так и дискретной (например, 
).
Как найти 
?
Пусть имеется непрерывная случайная величина с 
.
Пусть функция 
— строго монотонна, непрерывна и дифференцируема на отрезке 
, и 
, т. е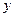 
существует только при 
.
Тогда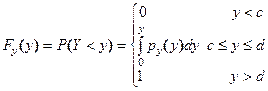 
J Воспоминания об обратных функциях:
При 
: 
Для нахождения плотности распределения возьмем производные по переменному верхнему пределу
:
.
Модуль появляется, так как 
, а если 
убывающая, то и 
— убывающая и производная отрицательна.
|
Пусть 
известна и 
—линейная функция. Линейная зависимость монотонна. Найдем 
.
V 
Найти , если 
.
Ï 
N
V 
Найти , если 
, 
.
Ï 
N
Дата публикования: 2015-10-09; Прочитано: 472 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
