Корреляция

Пусть — двумерная CB. Корреляционный момент (ковариация)

Для дискретных СВ:

, где .

Для непрерывных СВ:

, где 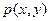-совместная плотность распределения СВ .

Корреляционный момент характеризует степень линейной зависимости СВ и .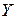

Свойства корреляционного момента

1. :

.

2. Для независимых CB корреляционный момент равен 0:

3. /

4.

Доказательство.

Очевидно:

.

,

.

5. тогда и только тогда, когда 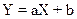(X и Y связаны линейной зависимостью).

6. Если , то

:

.

Следствие.

Если то

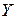Для независимых CB корреляционный момент равен 0. Но если 0, не следует, что CB и независимы.

Ковариационной матрицей (матрицей ковариаций) n -мерной CB называется матрица :

			…
			…
			…
…	…	…	…	…
			…

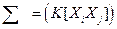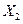
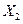
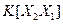
Уточненные свойства математического ожидания и дисперсии

1. Для независимых СВ

.

В общем случае

.

Это следует из свойства 3: .

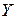Если CB и независимы, то .

2. Для независимых СВ

.

В общем случае

Покажем это.

= .

Для n СВ:

.