Плотность вероятности является непрерывной функцией

Плотность вероятности имеет размерность случайной величины.

Рассмотрим числовые характеристики непрерывных случайных величин.

Смысл математического ожидания и дисперсии остается таким же, как и случае дискретных случайных величин. Меняется вид формул для их нахождения путем замены:

Тогда получаем формулы для расчета математического ожидания и дисперсии непрерывной случайной величины:

, где

ПРИМЕР. (Равномерное распределение). Рассмотрим непрерывную случайную величину Х, возможные значения которой лежат в некотором интервале и равновероятны. Плотность вероятности такой случайной величины будет иметь вид:

- равномерное распределение.

Где с - некоторая постоянная.

График плотности вероятности изобразится следующим образом:

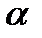
Выразим параметр С через α и β. Для этого используем тот факт, что интеграл от плотности вероятности по всей области должен быть равен 1:

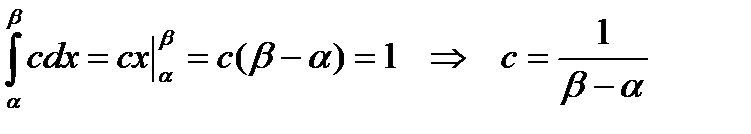
Имеем:

- плотность вероятности равномерно распределенной случайной величины.

Найдем функцию распределения:

- функция распределения равномерно распределенной случайной величины.

Построим график функции распределения:

Вычислим математическое ожидание, дисперсию и среднее квадратичное отклонение случайной величины, подчиняющейся равномерному распределению.

Тогда среднеквадратичное отклонение будет иметь вид:

В рассмотренном примере мы выражали функцию распределения из заданной плотности вероятности. Теперь рассмотрим обратную задачу – найти плотность вероятности из функции распределения.

ПРИМЕР. (Показательное распределение). Пусть непрерывная случайная величина Х задана функцией распределения - функция распределения случайной величины, распределенной по показательному закону.

График функции распределения имеет вид:

Найдем плотность вероятности этой случайной величины. Плотность вероятности находится как производная от функции распределения:

- плотность вероятности случайной величины, распределенной по показательному закону.

Кривая распределения имеет вид:

Найдем математическое ожидание, дисперсию и среднее квадратичное распределение случайной величины, распределенной по показательному закону.

Полученный определенный интеграл будем брать по частям:

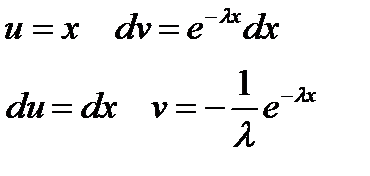
Первые два слагаемых в пределе равны 0, т.к. экспонента в минус бесконечной степени стремиться к 0.

Теперь найдем дисперсию.

Берем интеграл по частям:

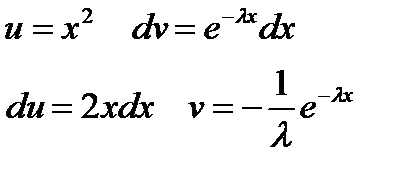
Полученный интеграл еще раз берем по частям: