 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Случайной величиной называется величина, которая в результате опыта принимает заранее неизвестное численное значение
|
|
Те значения, которые она может принимать в результате опыта, образуют множество ее возможных значений или спектр значений. Случайные величины бывают непрерывными и дискретными.
Будем обозначать случайные величины заглавными латинскими буквами, например, Х, а их возможные значения прописными буквами - х.
Например, пусть Х - число очков, выпавших при бросании кубика. Х - случайная величина и множество ее значений будет:
{1,2,3,4,5,6}.
Случайная величина называется дискретной, если множество ее возможных значений cчетно (т.е. все возможные значения можно пронумеровать натуральными числами):
 .
.
Дискретная случайная величина полностью определяется своим рядом распределения.
Ряд распределения представляет собой таблицу, в первой строке которой указаны все возможные значения случайной величины, а во второй - их вероятности:

| 
| 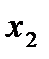
| … | 
|

| 
| 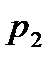
| … | 
|
Поскольку ряд распределения содержит все возможные значения случайной величины, то суммарная вероятность должна быть равна 1.
По ряду распределения можно находить различные вероятности и строить многоугольник распределения.
Многоугольник распределения – ломаная, которая соединяет точки, абсциссы которых содержит первая строка ряда распределения (значения случайной величины), а ординаты – вторая строка (вероятности этих значений).
ПРИМЕР. Происходит опыт с бросанием двух игральных кубиков. Пусть случайная величина Х - сумма выпавших очков. Составить для нее ряд распределения, построить многоугольник распределения и найти вероятности:  .
.
РЕШЕНИЕ:
Если случайная величина Х - сумма выпавших очков при бросании двух кубиков, то ее спектр возможных значений имеет вид:
{2,3,4,5,6,7.8,9,10,11,12}.
Найдем вероятности этих значений.
Общее число всех возможных случаев n=36. Значению Х=2 благоприятен один случай, когда на обоих кубиках выпадает по одному очку (1;1), следовательно, m=1. Тогда по классической формуле подсчета вероятностей:
 .
.
Значению Х=3 благоприятно два случая: (1;2) и (2;1), следовательно, m=2. Тогда:
 .
.
Значению Х=4 благоприятно три случая: (2;2), (3;1), (1;3), следовательно, m=3. Тогда:
 .
.
Значению Х=5 благоприятно четыре случая: (2;3), (3;2), (1;4), (4;1), следовательно, m=4. Тогда:
 .
.
Значению Х=6 благоприятно пять случаев: (3;3), (4;2), (2;4), (5;1), (1;5), следовательно, m=5. Тогда:
 .
.
Значению Х=7 благоприятно шесть случаев: (3;4), (4;3), (2;5), (5;2), (1;6), (6;1), следовательно, m=6. Тогда:
 .
.
Значению Х=8 благоприятно пять случаев: (3;5), (5;3), (2;6), (6;2), (4;4), следовательно, m=5. Тогда:
 .
.
Значению Х=9 благоприятно четыре случая: (6;3), (3;6), (5;4), (4;5), следовательно, m=4. Тогда:
 .
.
Значению Х=10 благоприятно три случая: (5;5), (4;6), (6;4), следовательно, m=3. Тогда:
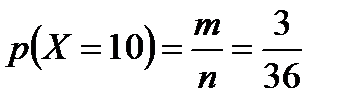 .
.
Значению Х=11 благоприятно два случая: (5;6) и (6;5), следовательно, m=2. Тогда:
 .
.
Значению Х=2 благоприятен один случай: (6;6), следовательно, m=1. Тогда:
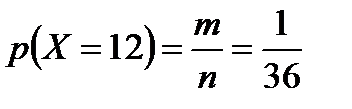 .
.
Составляем ряд распределения:

| |||||||||||

| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
|
Можно убедиться, что суммарная вероятность в таблице равна 1.
Теперь построим многоугольник распределения:




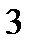




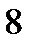










Теперь найдем искомые вероятности:



Кроме ряда распределения, дискретные случайные величины имеют несколько числовых характеристик. Рассмотрим их.
Математическим ожиданием M[X] дискретной случайной величины Х называется сумма ряда

Например, в рассмотренном выше примере с двумя игральными кубиками:
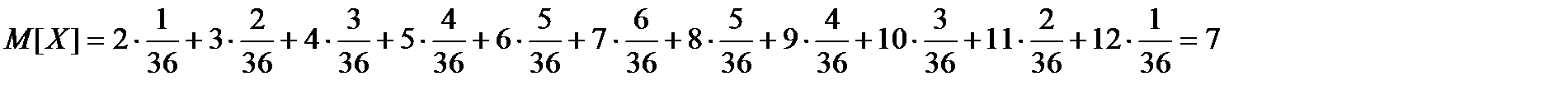
Свойства математического ожидания
1. Математическое ожидание от постоянной величины равно этой постоянной величине:
М[C]=C, C=const.
2. Математическое ожидание суммы случайных величин Х и У равно сумме математических ожиданий этих величин:
М[X+Y]=M[X]+M[Y].
3. Математическое ожидание суммы случайной величины Х и постоянной величины С равно сумме математического ожидания Х и самой величины С:
М[X+С]=M[X]+С.
4. Постоянную величину можно выносить за знак математического ожидания:
М[k X]=k M[X], где k=cоnst.
5. Математическое ожидание произведения независимых случайных величин Х и У равно произведению математических ожиданий этих величин:
М[XY]=M[X]M[Y].
Другая характеристика случайных величин называется дисперсией.
Дисперсия - это мера рассеяния значений случайной величины около ее математического ожидания:

Для вычисления дисперсии часто используют другую формулу:

Вычислим дисперсию для случайной величины из предыдущего примера. Сначала воспользуемся определением дисперсии:
 Теперь воспользуемся другой формулой для дисперсии;
Теперь воспользуемся другой формулой для дисперсии;



Естественно, что результат получился одинаковым.
Свойства дисперсии
1. Дисперсия от постоянной величины равна нулю:
D[C]=0, C=const.
2. Дисперсия суммы случайной величины Х и постоянной величины С равна дисперсии величины Х:
D[X+С]=D[X].
3. Постоянная величина выносится за знак дисперсии в квадрате: 
4. Дисперсия всегда неотрицательна:
 .
.
Наконец, еще одна характеристика случайных величин – среднее квадратичное отклонение.
Квадратный корень из дисперсии называется средним квадратичным отклонением:

Дисперсия имеет размерность квадрата случайной величины, а среднее квадратичное отклонение имеет размерность самой случайной величины.
Рассмотрим еще один пример. Пусть даны две дискретные случайные величины Х и У, заданные своими рядами распределения:

| -1 | ||

| 0.3 | 0.3 | 0.4 |

| |||

| 0.2 | 0.4 | 0.4 |
Найти законы распределения случайных величин:  .
.
Сначала найдем закон распределения  . Для этого составим таблицу, в которой перечислим все возможные значения этой величины в зависимости от значений Х, и соответствующие им вероятности:
. Для этого составим таблицу, в которой перечислим все возможные значения этой величины в зависимости от значений Х, и соответствующие им вероятности:
| Х | 
| 
|
| -1 | 0.3 | |
| 0.3 | ||
| 0.4 |
Теперь на основании этой таблицы составляем ряд распределения случайной величины  . При этом учтем, что значение 1 встречается в таблице дважды (с вероятностями 0.3 и 0.4), поэтому в ряд распределения мы запишем его один раз с вероятностью 0.3+0.4=0.7:
. При этом учтем, что значение 1 встречается в таблице дважды (с вероятностями 0.3 и 0.4), поэтому в ряд распределения мы запишем его один раз с вероятностью 0.3+0.4=0.7:

| ||

| 0.3 | 0.7 |
Как и следовало ожидать, суммарная вероятность получилась равна 1.
Далее составим ряд распределения для величины 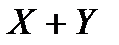 :
:
| Х | У | Х+У | 
|
| -1 | 
| ||
| -1 | 
| ||
| -1 | 
| ||

| |||

| |||

| |||

| |||

| |||

|
Теперь на основании этой таблицы составляем ряд распределения случайной величины  . При этом учтем повторяющиеся значения (запишем в ряд распределения одно значение с вероятностью, равной сумме вероятностей этих одинаковых значений):
. При этом учтем повторяющиеся значения (запишем в ряд распределения одно значение с вероятностью, равной сумме вероятностей этих одинаковых значений):

| |||||

| 0.06 | 0.18 | 0.32 | 0.28 | 0.16 |
Далее составим ряд распределения для величины  :
:
| Х | У | Х+У | 
|
| -1 | -1 | 
| |
| -1 | -2 | 
| |
| -1 | -3 | 
| |

| |||

| |||

| |||

| |||

| |||

|
Теперь на основании этой таблицы составляем ряд распределения случайной величины  :
:

| -3 | -2 | -1 | ||||

| 0.12 | 0.12 | 0.06 | 0.3 | 0.08 | 0.16 | 0.16 |
Введем еще одну характеристику случайной величины – функцию распределения.
Рассмотрим вероятность того, что СВ Х примет значение, меньшее, чем х, т.е. Р(Х<х) – эта величина называется функцией распределения:
 .
.
Свойства функции распределения
1. Функция распределения является неубывающей функцией своего аргумента, т.е. если
 .
.
2. На минус бесконечности функция распределения равна нулю:
 .
.
3. На плюс бесконечности функция распределения равна единице:
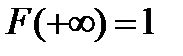 .
.
Дата публикования: 2015-10-09; Прочитано: 1788 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
